AT_agc050_f [AGC050F] NAND Tree

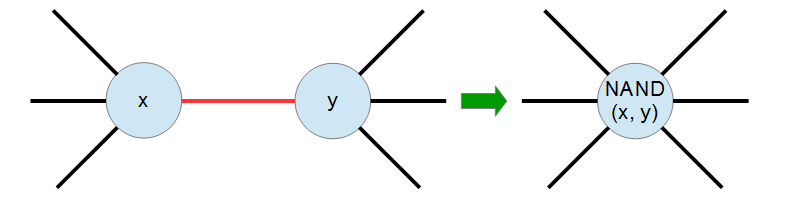
有一棵树，每个顶点上写有 $0$ 或 $1$。这棵树有 $N$ 个顶点，编号为 $1$ 到 $N$。对于每个 $i$，存在一条连接顶点 $a_i$ 和顶点 $b_i$ 的边。顶点 $i$ 上写的数字为 $c_i$。 すぬけ君会对这棵树重复以下操作： - 选择一条边进行缩约，将被消去的两个顶点上的数字进行 NAND 运算，并将结果写在新顶点上。  经过 $N-1$ 次操作后，树会只剩下一个顶点。在所有 $(N-1)!$ 种操作顺序中，最后剩下的顶点上写有 $1$ 的方案有多少种？请计算这个答案对 $2$ 取余的结果。

输入从标准输入读入，格式如下： > $N$ $a_1$ $b_1$ $:$ $a_{N-1}$ $b_{N-1}$ $c_1$ $c_2$ $\cdots$ $c_N$

请输出答案。

### 注释 - NAND 运算的定义如下：$NAND(0, 0) = NAND(0, 1) = NAND(1, 0) = 1,\quad NAND(1, 1) = 0$。 - 当缩约连接顶点 $s$ 和顶点 $t$ 的边时，要同时去除该边并合并这两个顶点。缩约后的树中，如果合并产生的新顶点与顶点 $u$ 之间存在边，当且仅当缩约前的树中 $s$ 与 $u$ 有边或 $t$ 与 $u$ 有边。 ### 数据范围 - $2 \leq N \leq 300$ - $1 \leq a_i < b_i \leq N$ - 输入描述的图是一棵树。 - $0 \leq c_i \leq 1$ - 输入中的所有值均为整数。 ### 样例解释 1 在 $6$ 种操作顺序中，有 $4$ 种情况下最后剩下的顶点上写有 $1$。因此答案为 $4 \bmod 2 = 0$。 由 ChatGPT 4.1 翻译