AT_agc050_f [AGC050F] NAND Tree

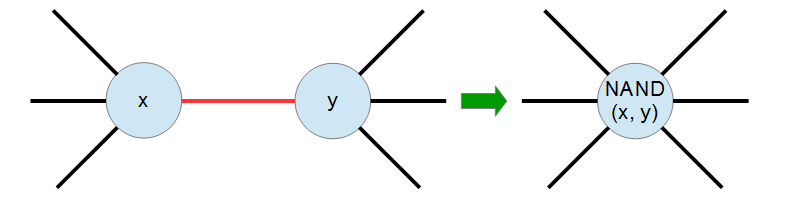
[problemUrl]: https://atcoder.jp/contests/agc050/tasks/agc050_f 各頂点に $ 0 $ または $ 1 $ が書かれた木があります。 この木は $ N $ 個の頂点を持ち、それらには $ 1 $ から $ N $ までの番号が振られています。 各 $ i $ について、頂点 $ a_i $ と頂点 $ b_i $ を結ぶ辺が存在します。 頂点 $ i $ に書かれた数は $ c_i $ です。 すぬけ君は、この木に以下の操作を繰り返します。 - 辺を $ 1 $ 本選んで縮約し、消された $ 2 $ 個の頂点に書かれていた数の NAND を新たな頂点に書き込む。  $ N\ -\ 1 $ 回の操作後、木は $ 1 $ 個の頂点となります。 このような操作の行い方は $ (N-1)! $ 通りありますが、そのうち最後の頂点に $ 1 $ が書き込まれるものは何通りあるでしょうか。 この答えを **$ 2 $ で割った余り**を計算してください。

入力は標準入力から以下の形式で与えられる。 > $ N $ $ a_1 $ $ b_1 $ $ : $ $ a_{N-1} $ $ b_{N-1} $ $ c_1 $ $ c_2 $ $ \cdots $ $ c_N $

答えを出力せよ。

### 注記 - 演算 NAND の定義は次の通りです: $ NAND(0,\ 0)\ =\ NAND(0,\ 1)\ =\ NAND(1,\ 0)\ =\ 1,\ NAND(1,\ 1)\ =\ 0 $. - 頂点 $ s $ と頂点 $ t $ を結ぶ辺を縮約する際は、その辺を取り除くと同時に $ 2 $ 頂点を併合します。 縮約後の木において、併合により生まれた頂点と頂点 $ u $ を結ぶ辺が存在するのは、縮約前の木において $ s $ と $ u $ を結ぶ辺または $ t $ と $ u $ を結ぶ辺が存在するときであり、またそのときに限られます。 ### 制約 - $ 2\ \leq\ N\ \leq\ 300 $ - $ 1\ \leq\ a_i\