AT_agc051_b [AGC051B] Bowling

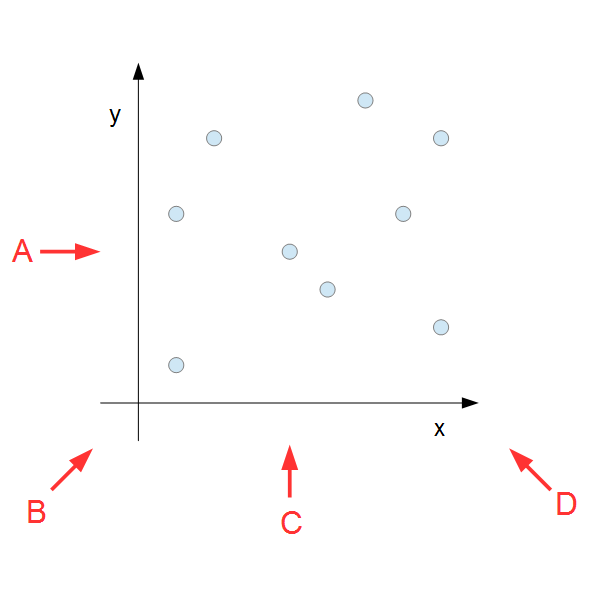
平面上竖立着若干个保龄球瓶，有 4 个人从不同的角度观察它们。是否存在一种情况，使得只有 1 个人能看到远多于其他人的瓶子？ 我们可以将瓶子简单地视为 $xy$ 平面上的点集。4 个人的位置如下图所示。具体来说： - 从 **A** 的视角看，$y$ 坐标相同的两个瓶子会重叠。 - 从 **B** 的视角看，($x$ 坐标 $-$ $y$ 坐标) 相同的两个瓶子会重叠。 - 从 **C** 的视角看，$x$ 坐标相同的两个瓶子会重叠。 - 从 **D** 的视角看，($x$ 坐标 $+$ $y$ 坐标) 相同的两个瓶子会重叠。  分别记 **A**、**B**、**C**、**D** 能看到的瓶子数为 $a,\ b,\ c,\ d$。 请构造一种瓶子的摆放方式，使其同时满足以下所有条件： - $d \geq 10 \cdot \max\{a, b, c\}$ - 瓶子的总数不少于 1 个且不超过 $10^5$ 个。 - 所有瓶子的坐标均为 $0$ 以上、$10^9$ 以下的整数。 - 不允许有两个瓶子处于同一位置。

无输入。

请按以下格式输出答案，其中 $N$ 为瓶子的总数，$(x_i, y_i)$ 为第 $i$ 个瓶子的坐标。 > $N$ $x_1$ $y_1$ $:$ $x_N$ $y_N$ 输出必须满足题目中的所有条件。

### 样例解释 1 **此输出仅为输出格式示例，并非正确答案。** 该输出对应于题目中的图，$d = 8, a = b = c = 7$。虽然已经很努力了，但还未能通过 AC。 由 ChatGPT 4.1 翻译