AT_agc051_d [AGC051D] C4

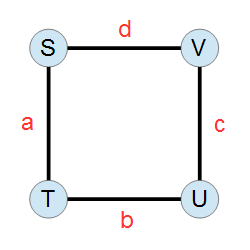
在如下的无向图中，求从 $S$ 出发回到 $S$ 的所有路径（Walk）的数量，要求每条边 $ST$、$TU$、$UV$、$VS$ 分别经过 $a$、$b$、$c$、$d$ 次（不区分方向）。请将答案对 $998244353$ 取模后输出。 

输入从标准输入读入，格式如下： > $a$ $b$ $c$ $d$

输出满足条件的路径数量，对 $998244353$ 取模后的结果。

## 注释 从 $S$ 出发回到 $S$ 的路径（Walk），指的是顶点序列 $v_0 = S, v_1, \ldots, v_k = S$，对于每个 $i\ (0 \leq i < k)$，$v_i$ 与 $v_{i+1}$ 之间存在一条边。两条路径如果顶点序列不同，则视为不同的路径。 ## 约束 - $1 \leq a, b, c, d \leq 500000$ - 输入的所有值均为整数。 ## 样例解释 1 满足条件的路径共有 $10$ 条，其中一种为 $S \rightarrow T \rightarrow U \rightarrow V \rightarrow U \rightarrow T \rightarrow S \rightarrow V \rightarrow S$。 由 ChatGPT 4.1 翻译