AT_agc070_e [AGC070E] Remove 2K+1 Edges

You are given positive integers $ N $ and $ K $ . Consider an undirected tree $ T $ with $ (2K + 1)N + 1 $ vertices labeled from $ 1 $ to $ (2K + 1)N + 1 $ . Among all such trees, find the number, modulo $ 998244353 $ , of trees that satisfy the following condition. - It is possible to remove all edges from $ T $ by repeating the following operation: - Choose a path of length $ 2K + 1 $ and remove all edges in it. Formally, choose a sequence of distinct vertices $ v_0, v_1, \dots, v_{2K+1} $ such that there exists an edge $ (v_i, v_{i+1}) $ for all $ i $ such that $ 0 \leq i \leq 2K $ , and remove the edge $ (v_i, v_{i+1}) $ for all $ i $ such that $ 0 \leq i \leq 2K $ .

The input is given from Standard Input in the following format: > $ N $ $ K $

Print the number, modulo $ 998244353 $ , of trees with $ (2K + 1)N + 1 $ vertices satisfying the condition.

### Sample Explanation 1 For example, consider a tree with edges $ (1, 2) $ , $ (2, 3) $ , $ (2, 4) $ , $ (2, 6) $ , $ (3, 7) $ , and $ (4, 5) $ . By doing the following steps, one can remove all edges from the tree, so it satisfies the condition in the problem statement: - Choose the path $ (1,2,4,5) $ and remove edges $ (1,2) $ , $ (2,4) $ , $ (4,5) $ . - Choose the path $ (6,2,3,7) $ and remove edges $ (6,2) $ , $ (2,3) $ , $ (3,7) $ .  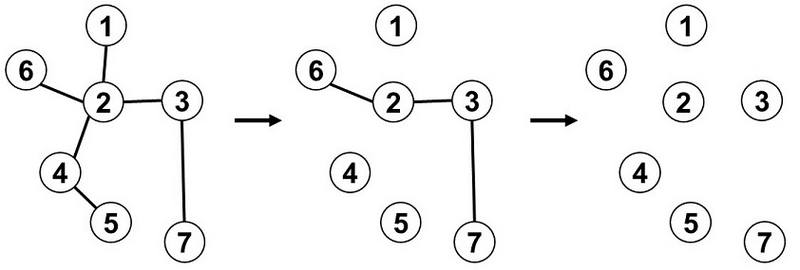There are $ 8820 $ such trees in total. ### Sample Explanation 2 Remember to print the count modulo $ 998244353 $ . ### Constraints - $ 1 \leq N \leq 1.3 \times 10^5 $ - $ 1 \leq K \leq 50 $ - All input values are integers.