AT_agc070_e [AGC070E] Remove 2K+1 Edges

正整数 $ N, K $ が与えられます。頂点に $ 1 $ から $ (2K + 1) N + 1 $ までの番号がついた $ (2K+1)N + 1 $ 頂点の無向木 $ T $ のうち次の条件を満たすものの個数を $ 998244353 $ で割った余りを求めてください。 - $ T $ に次の操作を繰り返し行うことで、 $ T $ に含まれる辺を全て取り除くことが出来る。 - 長さ $ 2K + 1 $ のパスを選び、パスに含まれる辺を全て取り除く。 厳密に述べると、相異なる頂点の列 $ v_0, v_1, \dots, v_{2K+1} $ であって $ 0 \leq i \leq 2K $ を満たす全ての $ i $ について辺 $ (v_i, v_{i+1}) $ が存在するものを選ぶ。そして、 $ 0 \leq i \leq 2K $ を満たす全ての $ i $ について辺 $ (v_i, v_{i+1}) $ を取り除く。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ K $

問題文の条件を満たす $ (2K + 1) N + 1 $ 頂点の無向木 $ T $ の個数を $ 998244353 $ で割った余りを出力せよ。

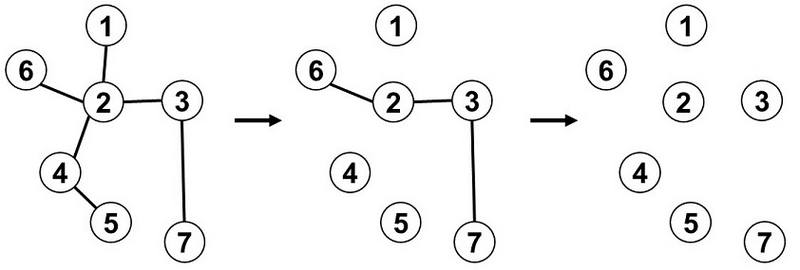
### Sample Explanation 1 例えば辺 $ (1, 2) $ , 辺 $ (2, 3) $ , 辺 $ (2, 4) $ , 辺 $ (2, 6) $ , 辺 $ (3, 7) $ , 辺 $ (4, 5) $ が存在する無向木を考えます。この木は以下の手順で操作を行うと全ての辺を取り除くことが出来るため、問題文の条件を満たします。 - パス $ (1,2,4,5) $ を選ぶ。辺 $ (1,2) $ , 辺 $ (2,4) $ , 辺 $ (4,5) $ を取り除く。 - パス $ (6,2,3,7) $ を選ぶ。辺 $ (6,2) $ , 辺 $ (2,3) $ , 辺 $ (3,7) $ を取り除く。  条件を満たす木は全部で $ 8820 $ 個あります。 ### Sample Explanation 2 個数を $ 998244353 $ で割った余りを出力する点に注意してください。 ### Constraints - $ 1 \leq N \leq 1.3 \times 10^5 $ - $ 1 \leq K \leq 50 $ - 入力される値は全て整数