AT_agc070_e [AGC070E] Remove 2K+1 Edges

给定正整数 $N$ 和 $K$，我们需要计算满足以下条件的无向树 $T$ 的数量，其中 $T$ 有 $(2K+1)N+1$ 个顶点，顶点编号从 $1$ 到 $(2K+1)N+1$，并且所有边都可以通过重复以下操作来移除： - 选择一条长度为 $2K+1$ 的路径，并移除该路径上的所有边。具体来说，选择一个由不同顶点组成的序列 $v_0, v_1, \dots, v_{2K+1}$，使得对于所有满足 $0 \leq i \leq 2K$ 的 $i$，边 $(v_i, v_{i+1})$ 都存在。然后，移除所有满足 $0 \leq i \leq 2K$ 的 $i$ 的边 $(v_i, v_{i+1})$。 我们需要计算满足上述条件的无向树 $T$ 的数量，并对结果取模 $998244353$。

输入包含两个整数 $N$ 和 $K$。

输出满足上述条件的 $(2K+1)N+1$ 个顶点的无向树 $T$ 的数量，并对结果取模 $998244353$。 ### 制约 - $1 \leq N \leq 1.3 \times 10^5$ - $1 \leq K \leq 50$ - 输入的所有值都是整数 ### 样例解释 1 例如，考虑一个无向树，其中存在边 $(1, 2)$, $(2, 3)$, $(2, 4)$, $(2, 6)$, $(3, 7)$, $(4, 5)$。通过以下步骤，我们可以移除所有边： - 选择路径 $(1,2,4,5)$，移除边 $(1,2)$, $(2,4)$, $(4,5)$。 - 选择路径 $(6,2,3,7)$，移除边 $(6,2)$, $(2,3)$, $(3,7)$。  因此，满足条件的无向树共有 $8820$ 个。 ### 样例解释 2 注意输出结果需要对 $998244353$ 取模。

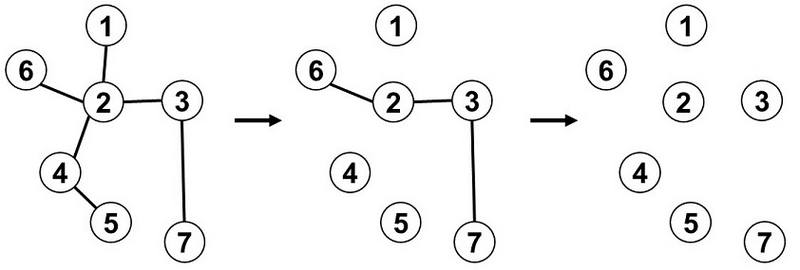
### Sample Explanation 1 例えば辺 $ (1, 2) $ , 辺 $ (2, 3) $ , 辺 $ (2, 4) $ , 辺 $ (2, 6) $ , 辺 $ (3, 7) $ , 辺 $ (4, 5) $ が存在する無向木を考えます。この木は以下の手順で操作を行うと全ての辺を取り除くことが出来るため、問題文の条件を満たします。 - パス $ (1,2,4,5) $ を選ぶ。辺 $ (1,2) $ , 辺 $ (2,4) $ , 辺 $ (4,5) $ を取り除く。 - パス $ (6,2,3,7) $ を選ぶ。辺 $ (6,2) $ , 辺 $ (2,3) $ , 辺 $ (3,7) $ を取り除く。  条件を満たす木は全部で $ 8820 $ 個あります。 ### Sample Explanation 2 個数を $ 998244353 $ で割った余りを出力する点に注意してください。 ### Constraints - $ 1 \leq N \leq 1.3 \times 10^5 $ - $ 1 \leq K \leq 50 $ - 入力される値は全て整数