AT_ahc038_a [AHC038A] Tree Robot Arm

[problemUrl]: https://atcoder.jp/contests/ahc038/tasks/ahc038_a $ N\times\ N $ マスのたこ焼き器がある。 一番左上のマスの座標を $ (0,0) $ とし、そこから下方向に $ i $ マス、右方向に $ j $ マス進んだ先のマスの座標を $ (i,j) $ とする。 初期状態で異なる $ M $ マスにたこ焼きが置かれており、 これらを指定された $ M $ マスの目的地に移動させたい。 まずはじめに、ロボットアームの設計を行う。 ロボットアームは「関節」と「指先」を頂点とし、その間を剛体の線分で結んだ木構造として表現される。 指先は木の葉に対応し、関節はそれ以外の頂点に対応する。 頂点 $ u $ とその子供 $ v $ を結ぶ辺の長さを $ L(u,v) $ と表記する。 使用可能なロボットアームの頂点数 $ V $ が指定されるので、頂点数が $ V $ 以下の木を設計し、根の初期位置とともに出力せよ。 木の各辺の長さ $ L(u,v) $ は、$ 1\leq\ L(u,v)\leq\ N-1 $ を満たす整数値でなければならない。 次に、設計したロボットアームを操作して、たこ焼きの移動を行う。 指定した初期位置に根があり、全ての辺が右方向に伸びた状態から開始して、毎ターン以下の操作を独立に行うことが出来る。 1. ロボットアーム全体を上下左右に1マス動かすことが出来る。移動後の根の座標 $ (x,y) $ は $ 0\leq\ x,y\leq\ N-1 $ を満たす必要がある。 2. 根以外の各頂点 $ u $ について独立に、$ u $ の親 $ p $ を軸として $ u $ 以下の部分木全体を反時計回りもしくは時計回りに90度回転させることが出来る。 3. 各指先について独立に、掴んでいるたこ焼きを現在のマスに置く、もしくは現在のマスに存在するたこ焼きを掴むことが出来る。すでにたこ焼きが置かれているマスや $ N\times\ N $ マスの範囲外にたこ焼きを置くことは出来ない。一つの指先で複数のたこ焼きを同時に掴むことも出来ない。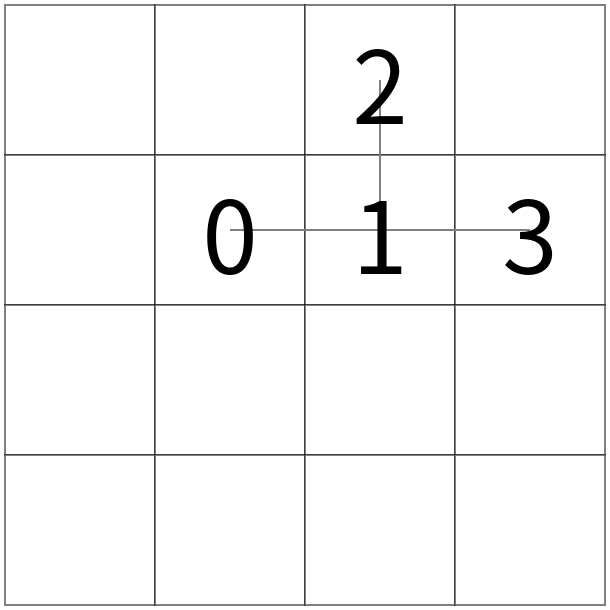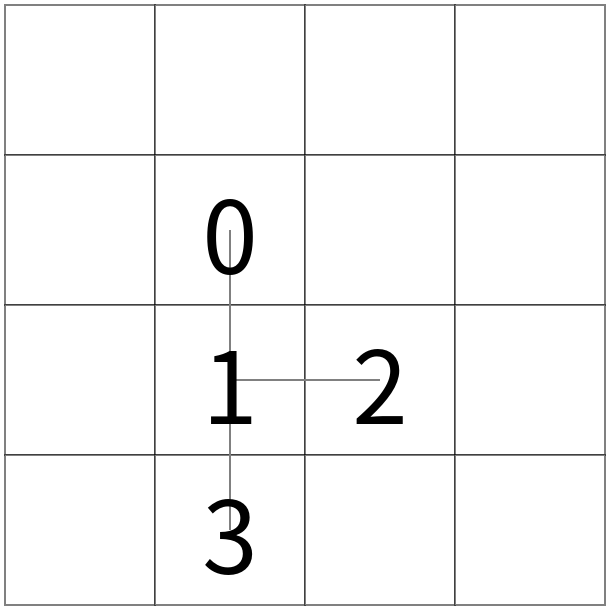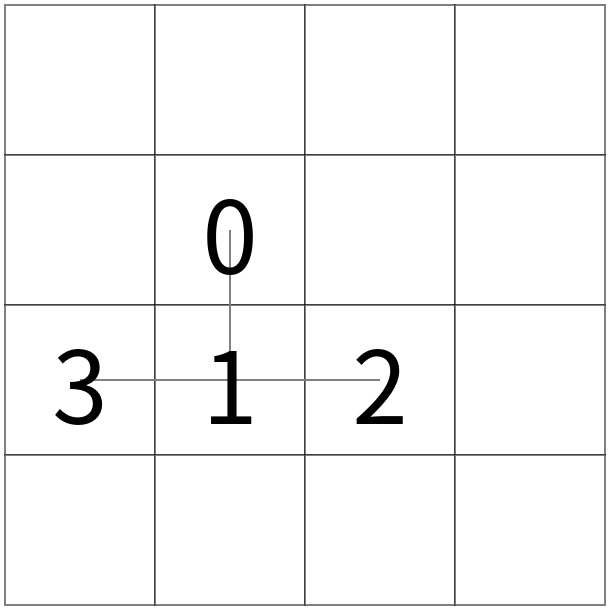 #### 操作2の例  ➡  ➡  左図から、頂点 $ 0 $ を軸として $ 1 $ 以下の部分木全体を時計回りに回転させると真ん中の図の状態となる。 更に、頂点 $ 1 $ を軸として $ 3 $ 以下の部分木全体を時計回りに回転させると右図の状態となる。 操作は 1 と 2 の後に 3 の順で行われ、操作 3 の中では頂点番号の小さい指先から順に処理が行われる (1、2 内の順番は操作後の状態に影響を与えない)。 操作後にロボットアームの一部が $ N\times\ N $ マスの外部にはみ出しても良く、ロボットアームの複数の頂点が同じマスを共有しても良い。 操作は最大で $ 10^5 $ ターン行うことが出来る。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ M $ $ V $ $ s_{0,0}\cdots\ s_{0,N-1} $ $ \vdots $ $ s_{N-1,0}\cdots\ s_{N-1,N-1} $ $ t_{0,0}\cdots\ t_{0,N-1} $ $ \vdots $ $ t_{N-1,0}\cdots\ t_{N-1,N-1} $ - グリッドの大きさ $ N $ は $ 15\leq\ N\leq\ 30 $ を満たす整数値である。 - たこ焼きの個数 $ M $ は $ N^2/10\leq\ M\leq\ N^2/2 $ を満たす整数値である。 - 使用可能なロボットアームの頂点数 $ V $ は $ 5\leq\ V\leq\ 15 $ を満たす整数値である。 - $ s_{i,0}\cdots\ s_{i,N-1} $ は `01` からなる $ N $ 文字の文字列であり、その $ j $ 文字目が `1` の場合、初期状態でマス $ (i,j) $ にたこ焼きが置かれていることを表す。たこ焼きが置かれているマスの個数はちょうど $ M $ である。 - $ t_{i,0}\cdots\ t_{i,N-1} $ は `01` からなる $ N $ 文字の文字列であり、その $ j $ 文字目が `1` の場合、マス $ (i,j) $ は目的地であることを表す。目的地であるマスの個数はちょうど $ M $ である。

設計したロボットアームの頂点数を $ V'(1\leq\ V'\leq\ V) $ とする。 頂点 $ 0 $ を根とし、頂点 $ u $ の親は $ u $ 未満となるよう、ロボットアームの各頂点に $ 0,\cdots,V'-1 $ の番号を振る。 頂点 $ u $ ($ 1\leq\ u\leq\ V'-1 $) の親を $ p_u $ ($ 0\leq\ p_u\leq\ u-1 $) とし、辺 $ (p_u,u) $ の長さを $ L(p_u,u) $ ($ 1\leq\ L(p_u,u)\leq\ N-1 $) とする。 初期状態における根の座標を $ (x,y) $ ($ 0\leq\ x,y\leq\ N-1 $) とする。 このとき、以下の形式で標準出力に出力せよ。 > $ V' $ $ p_1 $ $ L(p_1,1) $ $ \vdots $ $ p_{V'-1} $ $ L(p_{V'-1},V'-1) $ $ x $ $ y $ 次に、操作列を出力する。 1ターンの操作を以下のようにして $ 2V' $ 文字の文字列 $ S $ で表現する。 - $ 0 $ 文字目は、ロボットアーム全体を上下左右に1マス動かすならばそれぞれ、`U`、`D`、`L`、`R` であり、動かさないならば `.` である。 - $ i $ 文字目 ($ 1\leq\ i\leq\ V'-1 $) は、$ p_i $ を軸として頂点 $ i $ 以下の部分木全体を反時計回りに $ 90 $ 度回転させるならば `L`、時計回りに $ 90 $ 度回転させるならば `R`、何もしないならば `.`である。 - $ (V'+i) $ 文字目 ($ 0\leq\ i\leq\ V'-1 $) は、頂点 $ i $ が指先(葉)でないもしくは何もしないならば `.`、たこ焼きを掴むもしくは離すならば `P` である。 操作列の長さを $ T $、$ t $ ターン目の操作列を表す文字列を $ S_t $ としたとき、以下の形式で標準出力に出力せよ。 > $ S_0 $ $ \vdots $ $ S_{T-1} $ [例を見る](https://img.atcoder.jp/ahc038/GhBuR36w.html?lang=ja&seed=sample&output=sample)

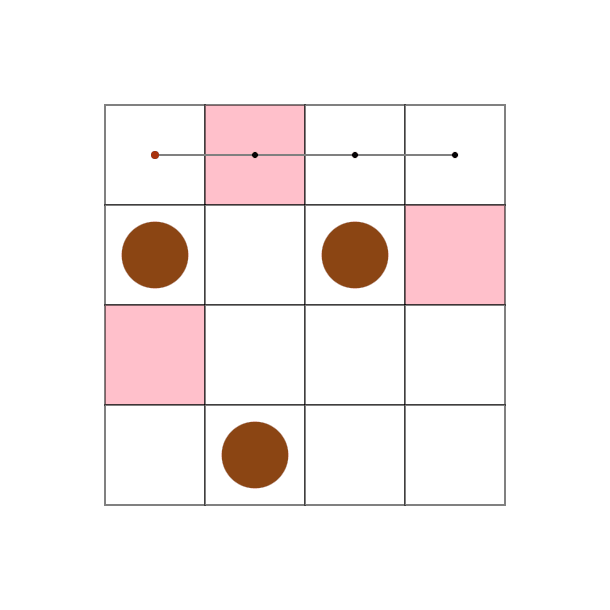
### ストーリー たこ焼きが大好きな高橋社長は、たこ焼きを移動させるロボットアームの開発をしている。 二次元グリッドで表現されたたこ焼き器上のいくつかのマスにたこ焼きが置かれている。 ロボットアームを用いて、これらのたこ焼きを指定されたマス集合へ移動させたい。 ロボットアームは複数の指先を持ち、関節と指先を頂点とした木構造で表現される。 一回の操作で、ロボットアーム全体を上下左右に動かす、関節を軸に90度回転させる、指先でたこ焼きを掴む、離す、という操作を同時に行うことが出来る。 操作ターン数が出来るだけ少なくなるようにロボットアームを設計し、操作方法を求めて欲しい。  ### 得点 操作ターン数を $ K $、操作終了時に目的地に存在するたこ焼きの個数を $ M' $ とする。 このとき、以下の絶対スコアが得られる。 **絶対スコアは小さければ小さいほど良い。** - $ M'=M $ の場合、$ K $ - $ M'\