AT_ajo2024_final_e Five Shuffles

有一棵包含 $N$ 个顶点的树。每个顶点编号为 $1$ 到 $N$，第 $i$ 条边 $(1 \leq i \leq N-1)$ 连接顶点 $u_i$ 和顶点 $v_i$。此外，每个顶点上写有一个 $1$ 到 $N$ 之间互不相同的整数，顶点 $i$ 上写的数是 $p_i$。 AtCoder 先生最多可以进行 $5$ 次如下所述的**独立集洗牌**操作。 > **独立集洗牌操作定义如下：** > > 首先，将树的所有顶点标记为白色，然后依次执行以下两步： > > 1. 选择某些顶点将其标记为黑色，但不能选择一条边连接的两个顶点都变黑； > 2. 将所有黑色顶点上的数进行任意重新排列。 进行操作后，如果能使至少 $N-2$ 个顶点满足：顶点 $i\ (1 \leq i \leq N)$ 上写的数为 $i$，就可以获得奖励。请给出一种实现这一目标的方法。题目保证在本问题的约束下，答案一定存在。

输入以如下格式从标准输入读入。 > $N$ $u_1$ $v_1$ $u_2$ $v_2$ $⋮$ $u_{N-1}$ $v_{N-1}$ $p_1$ $p_2$ $⋯$ $p_N$

请按以下格式输出答案。 设总共做了 $K$ 次独立集洗牌（$K \leq 5$），第 $i$ 次操作结束后，顶点 $j$ 上的数为 $a_{i,j}$。**不用保证操作次数最少。** > $K$ > $a_{1,1}$ $a_{1,2}$ $⋯$ $a_{1,N}$ > $a_{2,1}$ $a_{2,2}$ $⋯$ $a_{2,N}$ > $⋮$ > $a_{K,1}$ $a_{K,2}$ $⋯$ $a_{K,N}$

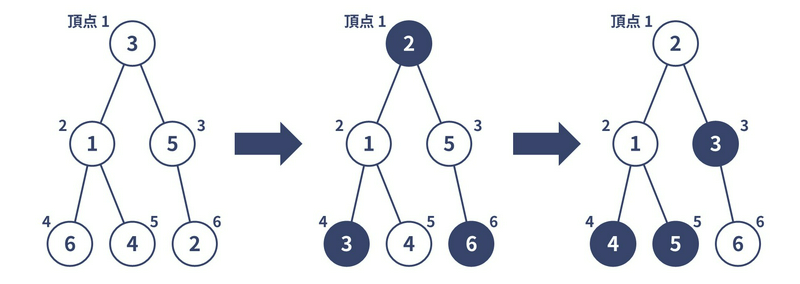
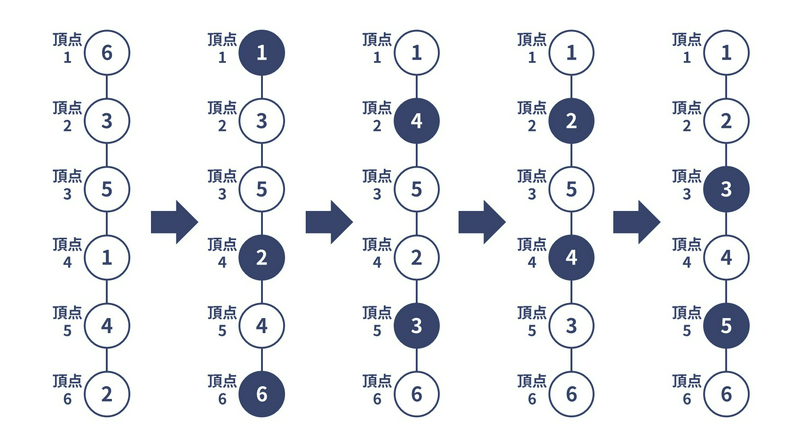
### 样例解释 1 例如，可以像下图这样操作，在不超过 $5$ 次的独立集洗牌内达成目标。注意，不需要使所有 $N$ 个顶点都满足 $i$ 号顶点上为 $i$。  ### 样例解释 2 例如，可以像下图这样操作，在不超过 $5$ 次的独立集洗牌内达成目标。  ### 数据范围 - $3 \leq N \leq 150\,000$ - $1 \leq u_i < v_i \leq N$ - $1 \leq p_i \leq N$ - $p_1, p_2, \dots, p_N$ 均互不相同 - 输入给定的图是一棵树 - 输入均为整数 由 ChatGPT 5 翻译