AT_ajo2024_final_e Five Shuffles

$ N $ 頂点の木があります。 頂点には $ 1 $ から $ N $ までの番号が付けられており、 $ i $ 番目の辺 $ (1 \leq i \leq N-1) $ は頂点 $ u_i $ と頂点 $ v_i $ を結んでいます。 また、各頂点には $ 1 $ 以上 $ N $ 以下の相異なる整数が書かれており、頂点 $ i $ $ (1 \leq i \leq N) $ に書かれた整数は $ p_i $ です。 AtCoder さんは、以下の**独立集合シャッフル**を高々 $ 5 $ 回行うことができます。 > **独立集合シャッフルとは** > > 木の各頂点をすべて白で塗った後、以下の 1 と 2 をその順に行う。 > > 1. 木のいくつかの頂点を黒で塗る。ただし、辺で隣接する $ 2 $ つの頂点の両方を黒で塗ってはならない。 > 2. 黒で塗られた頂点に書かれた整数を並べ替える。 操作の後、少なくとも $ N-2 $ 個の頂点について、頂点 $ i $ $ (1 \leq i \leq N) $ に書かれた整数を $ i $ にすることができればお金がもらえます。 そのような方法を $ 1 $ つ求めてください。 ただし、本問題の制約下では、必ず答えが存在することが証明できます。

入力は以下の形式で標準入力から与えられます。 > $ N $ $ u_1 $ $ v_1 $ $ u_2 $ $ v_2 $ $ \vdots $ $ u_{N-1} $ $ v_{N-1} $ $ p_1 $ $ p_2 $ $ \cdots $ $ p_N $

以下の形式で答えを出力してください。 ただし、行う独立集合シャッフルの回数を $ K $ $ (\leq 5) $ 、 $ i $ 回目の独立集合シャッフルの直後に頂点 $ j $ に書かれた整数を $ a_{i,j} $ とします。 ここで、**操作回数を最小化する必要はありません。** > $ K $ $ a_{1,1} $ $ a_{1,2} $ $ \cdots $ $ a_{1,N} $ $ a_{2,1} $ $ a_{2,2} $ $ \cdots $ $ a_{2,N} $ $ \vdots $ $ a_{K,1} $ $ a_{K,2} $ $ \cdots $ $ a_{K,N} $

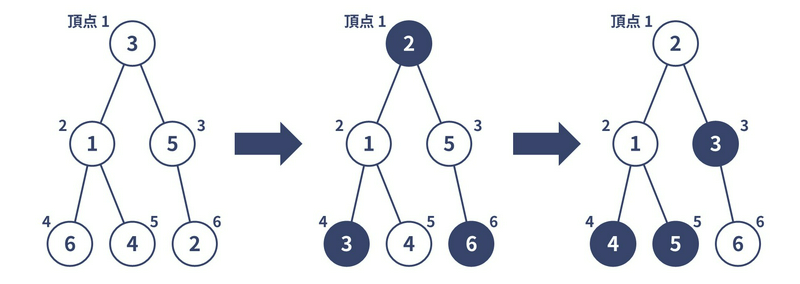
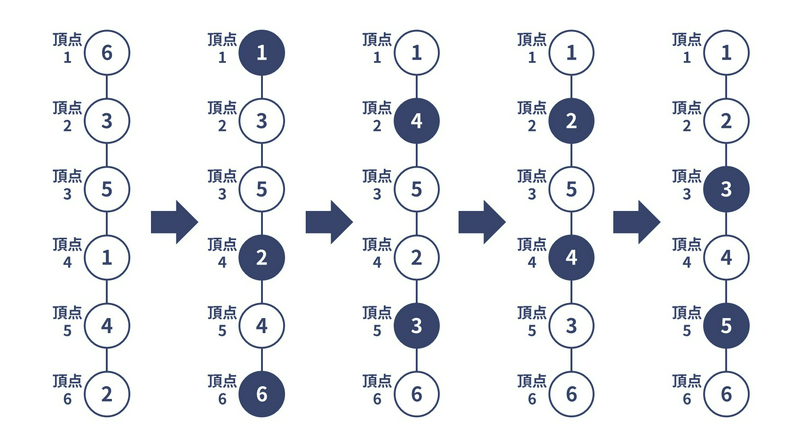
### Sample Explanation 1 たとえば下図のように操作を行うと、 $ 5 $ 回以内の独立集合シャッフルで目的を達成することができます。 なお、 $ N $ 頂点すべてについて頂点 $ i $ に書かれた整数を $ i $ にする必要はないことに注意してください。  ### Sample Explanation 2 たとえば下図のように操作を行うと、 $ 5 $ 回以内の独立集合シャッフルで目的を達成することができます。  ### Constraints - $ 3 \leq N \leq 150\,000 $ - $ 1 \leq u_i < v_i \leq N $ - $ 1 \leq p_i \leq N $ - $ p_1, p_2, \dots, p_N $ はすべて異なる - 入力で与えられるグラフは木である - 入力はすべて整数