AT_arc003_4 [ARC003D] シャッフル席替え

[problemUrl]: https://atcoder.jp/contests/arc003/tasks/arc003_4 高橋君が働くAtCoder社では、いつも $ 1 $ つの円形のテーブルの周囲に社員全員で座ってミーティングを行います。 それぞれお気に入りの席があるのでいつも席は同じなのですが、今日は席替えをすることにしました。 高橋君がランダムに $ 2 $ 人を選び場所を入れ替える動作を決められた回数行った後の席配置が新しい席配置になります。 しかし、残念なことにAtCoder社には隣り合わせにしてしまうとミーティング中におしゃべりをしてミーティングを邪魔してしまう $ 2 $ 人組が存在します。 高橋君は真面目なので、ミーティングが滞りなく行われるようにそのような $ 2 $ 人組は $ 1 $ 組も隣り合わせにしたくないと思っています。 席替えを行った後に、隣り合わせにしてはいけない $ 2 $ 人組が $ 1 $ 組も隣り合わない確率を求めなさい。 入力は以下の形式で与えられる。 > $ N $ $ M $ $ K $ $ A_{1} $ $ B_{1} $ $ A_{2} $ $ B_{2} $ : : : : $ A_{M} $ $ B_{M} $ - $ 1 $ 行目は、社員の総数として整数 $ N\ (2\ ≦\ N\ ≦11 $)、隣り合わせにしてはいけない $ 2 $ 人組の組数として整数 $ M\ (0\ ≦\ M\ ≦\ 10) $、入れ替える回数として整数 $ K\ (0\ ≦\ K\ ≦\ 20) $ が空白で区切られて与えられる。 - $ 2 $ 行目から $ M $ 行は、$ 1 $ 行に $ 1 $ 組ずつ隣り合わせにしてはいけない $ 2 $ 人が空白で区切られて与えられる。 - $ i+1 $ 行目の整数 $ A_{i} $ と整数 $ B_{i} $ ($ 0\ ≦\ A_{i}\ )\ は、隣り合わせにしてはいけない\ 2 $ 人を表し、それぞれ高橋君から見て右に何人目であるかを表す。 - なお $ A_i\ =\ 0 $ または、$ B_i\ =\ 0 $ の場合は高橋君自身を表す。 ちょうど $ K $ 回の入れ替えを行った後に、隣同士にしてはいけない $ 2 $ 人組が $ 1 $ 組も隣り合っていない確率を標準出力に $ 1 $ 行で出力せよ。 誤差は絶対誤差あるいは相対誤差の少なくとも片方が **$ 2e−3 $** 以下であれば許容する。 なお、最後には改行を出力せよ。 ```

4 1 1
0 3
```

 ```
0.333333333333
```

- 席替えを行う前は、$ 4 $ 人の配置は下図のようになっています。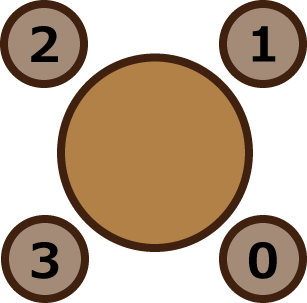
 ![](https://cdn.luogu.com.cn/upload/vjudge_pic/AT_arc003_4/61f407bc249a62aa28587ddc10de70ed39cd35f8.png)

- $ 1 $ 回入れ替えるという席変えを行った時、$ 0 $ と $ 3 $ の $ 2 $ 人が隣合わないようにするには、
- $ 0 $ と $ 1 $ を入れ替える。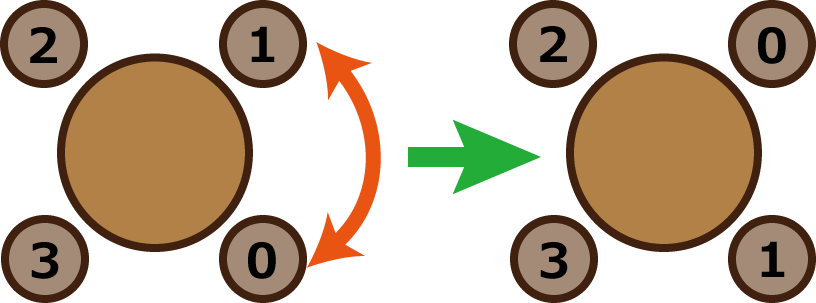
 ![](https://cdn.luogu.com.cn/upload/vjudge_pic/AT_arc003_4/b19286769fe6c7ecb9a5050f87e1e287f00c5c8a.png)

- $ 2 $ と $ 3 $ を入れ替える。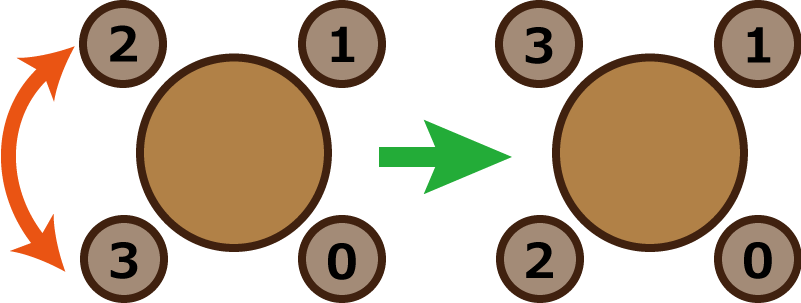
 ![](https://cdn.luogu.com.cn/upload/vjudge_pic/AT_arc003_4/61d023ca1bef08a0e0342606ed3ec6d425200be6.png)


- の $ 2 $ 通りです。$ 4 $ 人から $ 2 $ 人を選ぶ方法は $ 6 $ 通り存在するので、条件を満たす確率は $ 2/6 $ となり答えは $ 1/3 $ です。
 
```
5 4 20
0 1
0 2
0 3
0 4
```

 ```
0
```

- 高橋君以外の $ 4 $ 人のうち、高橋君と隣り合うことのできる人が $ 1 $ 人も存在しないので、条件を満たすことはありません。
 
```
5 1 2
0 3
```

 ```
0.52
```

- $ 2 $ 回の入れ替えの後、$ 0 $ と $ 3 $ が隣り合わない入れ替え方法は $ 52 $通りあります。
- $ 5 $ 人から $ 2 $ 人を選ぶことを $ 2 $ 回行うと全ての組み合わせは $ (_5C_2)^2\ =\ 10^2\ =\ 100 $ 通りになります。
- したがって、答えは $ 52÷100\ =\ 0.52 $ です。
                            

N/A

N/A