AT_arc004_1 [ARC004A] 2点間距離の最大値 ( The longest distance )
题目描述
平面上有 $N$ 个点,每个点编号从 $0$ 到 $N-1$,每个点给定其 $x$ 坐标和 $y$ 坐标。
请从这 $N$ 个点中任选两个点,连接成线段,求所有可能线段中最长的那一条的长度。输入按如下格式从标准输入读入。
> $N$ $x_{0}$ $y_{0}$ $x_{1}$ $y_{1}$ : : $x_{N-1}$ $y_{N-1}$
- 输入共 $N+1$ 行。
- 第 $1$ 行是一个整数 $N\ (2\leq N\leq 100)$,表示点的个数。
- 第 $2$ 行到第 $N+1$ 行的第 $i+1$ 行,给出第 $i$ 个点的 $x$ 坐标 $x_{i}(0\leq x_{i}\leq 100)$ 和 $y$ 坐标 $y_{i}(0\leq y_{i}\leq 100)$,以空格分隔。
- 不存在两个点的 $x$ 坐标和 $y$ 坐标都相同的情况,但可能存在某条线段上有其它点。
请输出所有可能线段中最长的那一条的长度,结果保留足够精度,保证绝对误差或相对误差至少有一项不超过 $10^{-3}$。
最后请输出换行符。
例如:
```
3
1 1
2 4
4 3
```
输出:
```
3.605551
```
- $3$ 个点的位置关系如下图所示。

- $(1,1)$ 和 $(2,4)$ 之间的线段长度为 $\sqrt{(2-1)^2+(4-1)^2} = \sqrt{10} = 3.162278$。
- $(2,4)$ 和 $(4,3)$ 之间的线段长度为 $\sqrt{(4-2)^2+(3-4)^2} = \sqrt{5} = 2.236068$。
- $(4,3)$ 和 $(1,1)$ 之间的线段长度为 $\sqrt{(1-4)^2+(1-3)^2} = \sqrt{13} = 3.605551$。
- 因此最长的线段长度为 $3.605551$。
```
10
1 8
4 0
3 7
2 4
5 9
9 1
6 2
0 2
8 6
7 8
```
输出:
```
10.630146
```
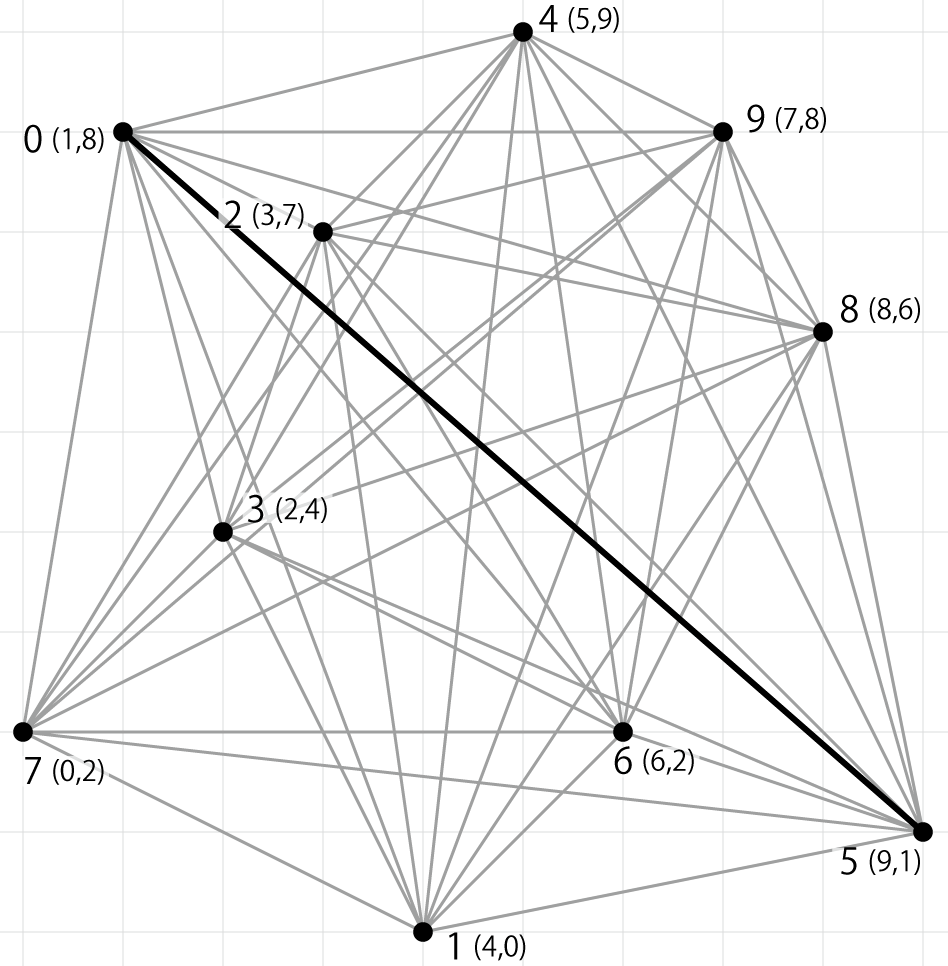
- $10$ 个点的位置关系如下图所示。
- 最长的线段是点 $0$ 和点 $5$ 之间,长度为 $10.630146$。
```
4
0 0
0 100
100 0
100 100
```
输出:
```
141.421356
```
- 最长的线段是点 $0$ 和点 $3$ 之间,或点 $1$ 和点 $2$ 之间,长度为 $141.421356$。
```
5
3 0
1 0
0 0
4 0
2 0
```
输出:
```
4.000000
```
- 最长的线段是点 $2$ 和点 $3$ 之间,长度为 $4.000000$。
```
4
2 2
0 0
1 1
3 3
```
输出:
```
4.242641
```
- 最长的线段是点 $1$ 和点 $3$ 之间,长度为 $4.242641$。
输入格式
第 $1$ 行包含一个整数 $N$,表示点的个数。
接下来 $N$ 行,每行包含两个整数 $x_{i}$ 和 $y_{i}$,表示第 $i$ 个点的坐标。
输出格式
输出一行,表示所有可能线段中最长的那一条的长度。
输出结果需保证绝对误差或相对误差至少有一项不超过 $10^{-3}$。
最后输出换行符。
说明/提示
- $2 \leq N \leq 100$
- $0 \leq x_{i}, y_{i} \leq 100$
- 不存在完全重合的点。
- 输出时请保证精度,建议输出至少 $6$ 位小数。
由 ChatGPT 4.1 翻译