AT_arc006_4 [ARC006D] アルファベット探し

[problemUrl]: https://atcoder.jp/contests/arc006/tasks/arc006_4 高橋君は友人にこのようなパズルを出題されました。 まず、図 $ 1 $ のような縦 $ 7 $ マス・横 $ 7 $ マスの $ 49 $ マスの白黒で作られた $ A,B,C $ の図形が与えられます。 図 $ 1 $：与えられる $ A,B,C $ の形 与えられる図の中に、先程の $ A,B,C $ の形がそれぞれいくつあるかを答えます。与えられる図に存在する黒マスは全て $ A,B,C $ のいずれかの一部であり、$ A,B,C $ 以外の図形は存在しません。 しかし、$ A,B,C $ は任意の正の整数倍に拡大した形も、同じ形とみなされます。そのため、図 $ 2(a) $ の $ 3 $ つの $ A $ は全て $ A $ として数えられます。 加えて、図 $ 2(b) $ のように、形が $ 90 $ 度きざみで回転しているものも同じ形とみなされます。 図 $ 2(a) $：$ 2 $ 倍、$ 3 $ 倍に拡大された $ A $ の例 図 $ 2(b) $：回転した $ A $ の例 なお、$ A,B,C $ の図形はまわりにある白マスの部分も含めてそのアルファベットと判断され、図 $ 3 $ のように $ A $ を構成する縦 $ 7 $ マス・横 $ 7 $ マスと、別の図形である $ B $ を構成する縦 $ 7 $ マス・横 $ 7 $ マスが重なるような入力は与えられません。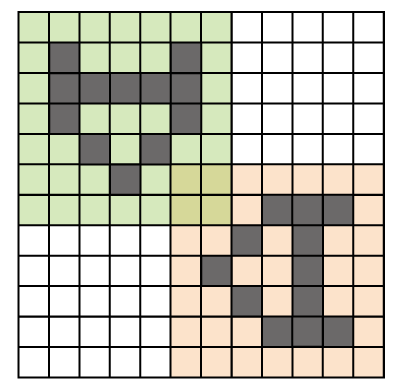 図 $ 3 $：入力として与えられない他の図形が重なっている例 与えられる図の中から、$ A,B,C $ の図形がそれぞれいくつずつあるか答えなさい。 入力は以下の形式で標準入力から与えられる。 > $ H $ $ W $ $ c_{(0,0)}c_{(0,1)} $ ‥‥ $ c_{(0,W-1)} $ $ c_{(1,0)}c_{(1,1)} $ ‥‥ $ c_{(1,W-1)} $ : : $ c_{(H-1,0)}c_{(H-1,1)} $ ‥‥ $ c_{(H-1,W-1)} $ - 入力は $ H+1 $ 行ある。 - $ 1 $ 行目には、与えられる図の縦の長さを表す整数 $ H(1≦H≦1,000) $ と横の長さを表す整数 $ W(1≦W≦1,000) $ が空白を区切りとして与えられる。 - $ 2 $ 行目からの $ H $ 行には、図の形を表す状態 $ c_{(i,j)}(0≦i≦H-1, $ $ 0≦j≦W-1) $ が与えられる。 - $ i-2 $ 行目 $ j-1 $ 番目の文字 $ c_{(i,j)} $ はそれぞれ `.` または `o` で与えられ、縦 $ i+1 $番目、横 $ j+1 $ 番目のマスの状態が以下であることを表す。 - `.`：そのマスが白色であることを表す。 - `o`：そのマスが黒色であることを表す。 - 図には $ A,B,C $ 以外の図形は出てこない。 - $ A,B,C $ の図形は重ならない。 与えられた図の中に存在する $ A $ の個数、$ B $ の個数、$ C $ の個数を、$ A,B,C $ の順に空白を区切りとして標準出力に $ 1 $ 行で出力せよ。 ただし、任意の正整数に等倍拡大した形や $ 90 $ 度きざみで回転した形も含まれる。 なお、最後には改行を出力せよ。 ``` 7 7 ....... ...o... ..o.o.. .o...o. .ooooo. .o...o. ....... ``` ``` 1 0 0 ``` - $ A $ が $ 1 $ つあり、$ B $ と $ C $ はありません。 ``` 7 14 .............. .oooo....oooo. .o...o..o...o. .oooo....oooo. .o...o..o...o. .oooo....oooo. .............. ``` ``` 0 2 0 ``` - 通常の向きの $ B $ が $ 1 $ つと、$ 180 $ 度回転している $ B $ が $ 1 $ つあるので、$ B $ が $ 2 $ つという答えになります。 ``` 14 42 .......................................... .................o...o........o.o......... ....oooooo.......ooooo.......o.o.o........ ....oooooo.......o...o.......o.o.o........ ..oo......oo......o.o........o.o.o........ ..oo......oo.......o.........ooooo........ ..oo...................................... ..oo...................................... ..oo......oo............ooo............... ..oo......oo...........o...o.............. ....oooooo.............o...o.............. ....oooooo.............o...o.............. ........................o.o............... .......................................... ``` ``` 1 1 2 ``` - $ 180 $ 度回転した $ A $、反時計回りに $ 90 $ 度回転した $ B $、時計回りに $ 90 $ 度回転した $ C $、$ 2 $ 倍に拡大した $ C $ が存在する。 ``` 6 8 ........ ........ ........ ........ ........ ........ ``` ``` 0 0 0 ``` - $ A,B,C $ が $ 1 $ つも存在しません。 ``` 40 40 ........................................ ..ooo.....o.................ooo......... .o...o...o.o....oooo.......o.o....o.o... .o......o...o..o...o......o..o...o...o.. .o...o..ooooo...oooo.......o.o...o...o.. ..ooo...o...o..o...o........ooo..o...o.. ................oooo..............ooo... ........................................ ...........................o.o.......... ..........................o.o.o......... .........ooo..............o.o.o......... ........o...o.............o.o.o......... ..ooo...o...o..ooooo......ooooo......... .o...o..o...o..o.o.o.................... .....o...o.o...o.o.o..............o.o... .o...o.........o.o.o.............o.o.o.. ..ooo...........o.o..............o.o.o.. .................................o.o.o.. .................................ooooo.. ...........................oooo......... ..........................o...o......... ...........................oooo......... .................ooo......o...o......... ................o...o......oooo......... ..oooooo........o....................... ..oooooo........o...o................... ....oo..oo.......ooo...............oooo. ....oo..oo........................o...o. ....oo....oo.......................oooo. ....oo....oo......................o...o. ....oo..oo.........................oooo. ....oo..oo.............................. ..oooooo................................ ..oooooo................ooo............. .................ooo.....o.o......o.o... ................o...o....o..o....o.o.o.. ................o........o.o.....o.o.o.. ................o...o...ooo......o.o.o.. .................ooo.............ooooo.. ........................................ ``` ``` 4 7 6 ```

N/A

N/A