AT_arc009_4 [ARC009D] 覚醒ノ高橋君

[problemUrl]: https://atcoder.jp/contests/arc009/tasks/arc009_4 AtCoder国には、たくさんの町が存在します。 町を管理するために、町の集合である、市が存在します。 市内の町と町は、道で結ばれています。これらの道によって、市内のすべての町に行き来できるようになっています。 ですが、これらの道だけでは他の市にある町に移動することが出来ません。 そこで、AtCoder国では、この問題を解決するためにいくつかの町を複数の市で管理することによって、市同士を繋げ、全ての市を行き来できるようにしています。 複数の市で１つの町を管理するのは非常に面倒なため、共有する数は、出来るだけ少なくなるようにされています。 具体的には、 $ N $ 個の市があるとして、 $ k $ 個の市で共有している町の個数を $ S_k $ とすると、 $ Σ(S_k×(k-1))=N-1 $ になります。 高橋君はAtCoder国の国土交通大臣で、各道の整備にかかるコストの総和を出来るだけ小さくしたいです。 ですが、整備計画が $ 1 $ つでは不安なので、 $ k $ 番目に良いプランまで考えることにしました。 そのプランの内容は以下の通りです。 - どの町の間を移動する場合にも、同じ町を重複して通らないように移動したとき、経路がちょうど $ 1 $ つに定まるように整備したいです。 - 道を整備するとは、町と町の間の道を減らすことである。 彼はこの条件を満たすプランがたくさんあることに気づきました。 そこで、プランのコストを、各道の整備にかかったコストの総和としました。 コストの値が小さい程、そのプランは良いと言えます。 $ k $ 番目に良いプランのコストを出力しなさい。$ k $番目の値が存在しない場合は$ -1 $を出力しなさい。 入力は以下の形式で標準入力から与えられる。 制約の追記を行いました> $ A $ $ T $ $ k $ $ N_1 $ $ C_{11} $ $ C_{12} $ $ C_{13} $ $ ... $ $ C_{1N_1} $ : : $ N_A $ $ C_{N1} $ $ C_{N2} $ $ C_{N3} $ $ ... $ $ C_{NN_A} $ $ M $ $ city_{11} $ $ city_{12} $ $ cost_1 $ : : $ cost_{M1} $ $ city_{M2} $ $ cost_M $ - 入力は $ 2×A+M+2 $ 行ある。 - $ 1 $ 行目には市の数 $ A(1≦A≦77) $ 、町の数 $ T(1≦T≦A×7) $ 、非負の整数 $ k(1≦k≦7,777,777) $ が与えられる。 - $ 2 $ 行目から $ 2×A+1 $ 行目までの $ 2×A $ 行は市に所属する町の情報が与えられる。 1. $ N_i(2≦N_i≦7) $ $ ... $ $ i $ 番目の市に所属する町の数を表す。 2. $ C_{ij}(1≦C_{ij}≦T) $ $ ... $ $ i $ 番目の市に所属する $ j $ 番目の町を表す。 12. $ M $ は道の数を表し、非負の整数である。入力の最後までの $ M $ 行は道の情報が与えられる。 1. $ city_{i1} $ と $ city_{i2} $ は $ i $ 番目の道が繋げている町を表す。つまり、 $ city_{i1} $ と $ city_{i2} $ は双方向に移動可能で、同じ市に属している。 2. $ cost_i(1≦cost_i≦77) $ は $ i $ 番目の道の整備にかかるコストを表す。 $ k $番目に良いプランのコストを出力しなさい。$ k $番目の値が存在しない場合は`-1`を出力しなさい。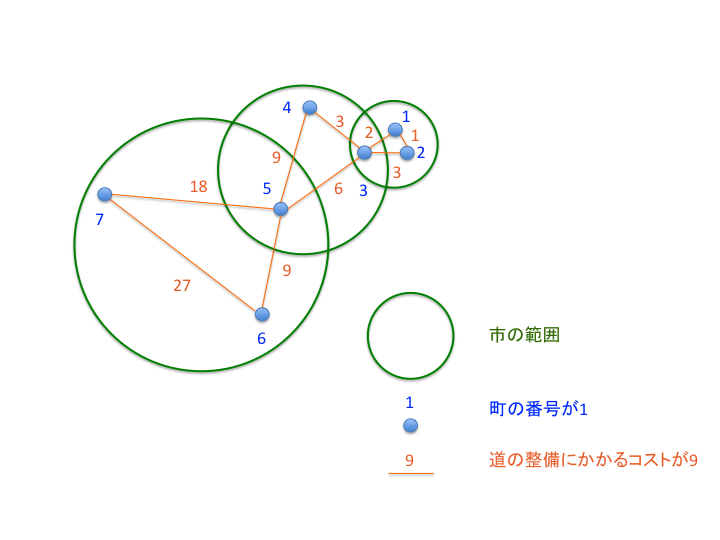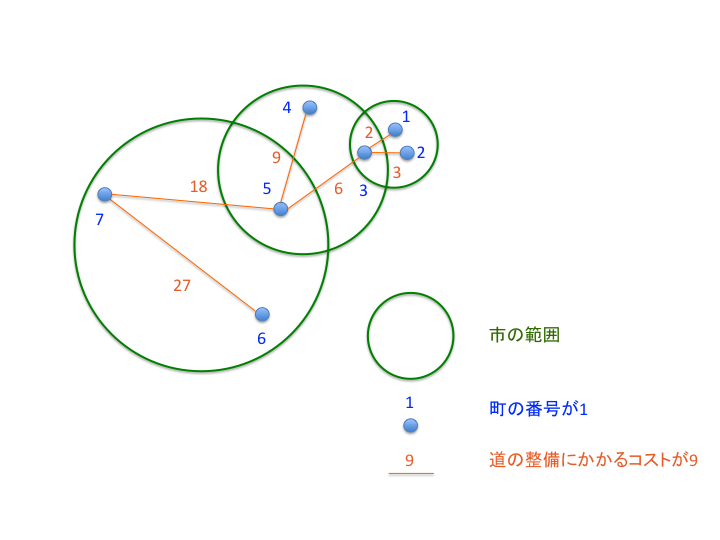 ``` 3 7 1 3 1 2 3 3 3 4 5 3 5 6 7 9 1 2 1 1 3 2 2 3 3 3 4 3 3 5 6 4 5 9 5 6 9 5 7 18 6 7 27 ``` 図：入力例 $ 1 $ を図示したもの ``` 13 ``` 図：出力例 $ 1 $ の状態を図示したもの - $ 1 $ 番目に良いプランは、町 $ 1 $ と 町 $ 2 $ を繋ぐ道、町 $ 3 $ と町 $ 4 $ を繋ぐ道、町 $ 5 $ と町 $ 6 $ を繋ぐ道を取り除いたプランです。 ``` 2 3 2 2 1 2 2 2 3 2 1 2 1 2 3 1 ``` ``` -1 ``` - $ 2 $ 番目に良いプランのコストが存在しないため、 `-1` を出力します。 ``` 4 9 2 3 1 2 3 3 3 4 5 3 5 6 7 3 5 8 9 12 1 2 1 1 3 1 2 3 1 3 4 3 3 5 3 4 5 3 5 6 6 5 7 3 6 7 9 5 8 9 5 9 18 8 9 27 ``` ``` 16 ``` - 合計コストが16のプランが最小ですが、これと同じコストで出来るプランは9通り存在します。よって、2番目のプランの必要コストも同じく16です。

N/A

N/A