AT_arc010_3 [ARC010C] 積み上げパズル

高桥君有一天决定玩如下的游戏。 有 $n$ 个按顺序掉落的方块，每个方块有 $m$ 种颜色。 每当有一个方块掉落时，高桥君可以选择将其放到唯一的“山”上，或者直接丢弃。 山上只能有一堆方块，且新放的方块必须放在最上面。 所有方块掉落完毕后，山的得分规则如下： - 颜色奖励：每种颜色有各自的得分，山上每有一个该颜色的方块，就获得该颜色的得分。 - 连击奖励：如果有 $x$ 个相同颜色的方块连续堆叠，则根据连击奖励分 $Y$，可以获得 $Y \times (x-1)$ 分。 - 全色奖励：如果山上每种颜色的方块都至少有一个，则额外获得 $Z$ 分。 给定掉落方块的种类和顺序，以及各项评分标准，请求出最高能获得的分数。输入格式如下： > $n$ $m$ $Y$ $Z$ $c_1$ $p_1$ $c_2$ $p_2$ $:$ $:$ $c_m$ $p_m$ $b_1b_2\ldots b_n$ - 第 $1$ 行为 $n,\ m,\ Y,\ Z$，用空格分隔。 1. $n$ 为方块总数，$1 \leq n \leq 5,000$。 2. $m$ 为颜色种类数，$1 \leq m \leq 10$。 3. $Y$ 为连击奖励分，$-100 \leq Y \leq 100$。 4. $Z$ 为全色奖励分，$-10,000 \leq Z \leq 10,000$。 5. $n,\ m,\ Y,\ Z$ 均为整数。 - 第 $2$ 行到第 $m+1$ 行，每行给出一种颜色的得分。 1. $c_i$ 表示第 $i$ 种颜色（大写英文字母）。 2. $p_i$ 表示 $c_i$ 的颜色奖励分，$-100 \leq p_i \leq 100$。 3. 不会有重复颜色。 - 第 $m+2$ 行给出长度为 $n$ 的字符串，表示掉落方块的颜色顺序。 1. $b_j$ 表示第 $j$ 个掉落方块的颜色，$b_j$ 只会是 $c_1,c_2,\ldots,c_m$ 中的一种。 请输出能获得的最大得分，并以一行输出，最后要换行。 例如： ``` 5 3 3 5 R 1 G 1 B 1 RGBRR ``` 输出： ``` 13 ``` - 如果全部方块都堆到山上： - 颜色奖励：每种颜色 $1$ 分，共 $5$ 个方块，$1 \times 5 = 5$ 分。 - 连击奖励：R 连续 $2$ 个，$3 \times (2-1) = 3$ 分。 - 全色奖励：三种颜色都出现，$5$ 分。 - 总分 $5+3+5=13$。 - 丢弃任意方块都不会更高，所以答案是 $13$。 ``` 3 3 3 5 R 1 G 3 B 2 RBR ``` 输出： ``` 5 ``` - 全部堆上去： - 颜色奖励：$1 \times 2 + 2 \times 1 = 4$ 分。 - 没有连击，没有全色奖励。 - 总分 $4$。 - 丢弃 B，只堆 RR： - 颜色奖励：$1 \times 2 = 2$ 分。 - 连击奖励：$3 \times (2-1) = 3$ 分。 - 总分 $5$，为最大值。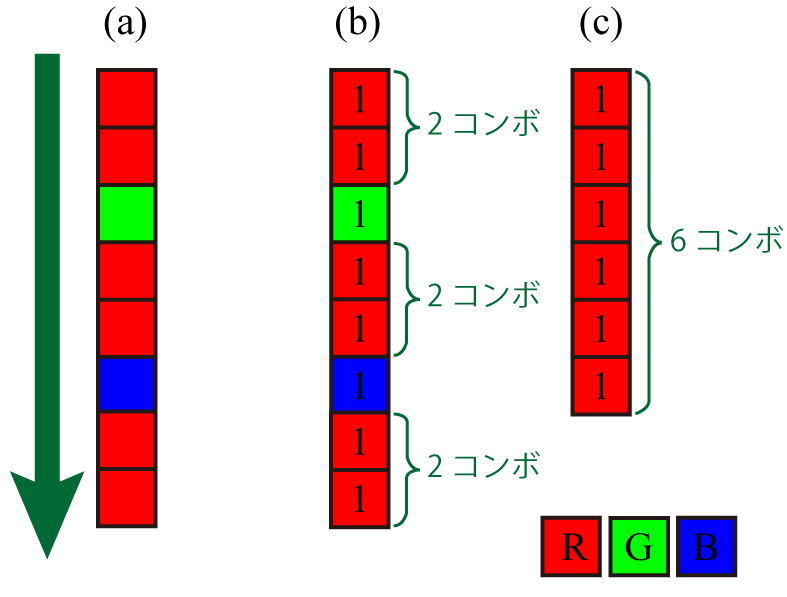 ``` 8 3 5 3 R 1 G 1 B 1 RRGRRBRR ``` 输出： ``` 31 ``` - 如图 (a)，顺序掉落 $8$ 个方块。 - 全部堆上去，图 (b)：有 $3$ 组 $2$ 连击，且有全色奖励。 - $1 \times 8 + 5 \times (2-1) \times 3 + 3 = 26$ 分。 - 只堆 R，图 (c)：$1 \times 6 + 5 \times (6-1) + 0 = 31$ 分，为最大值。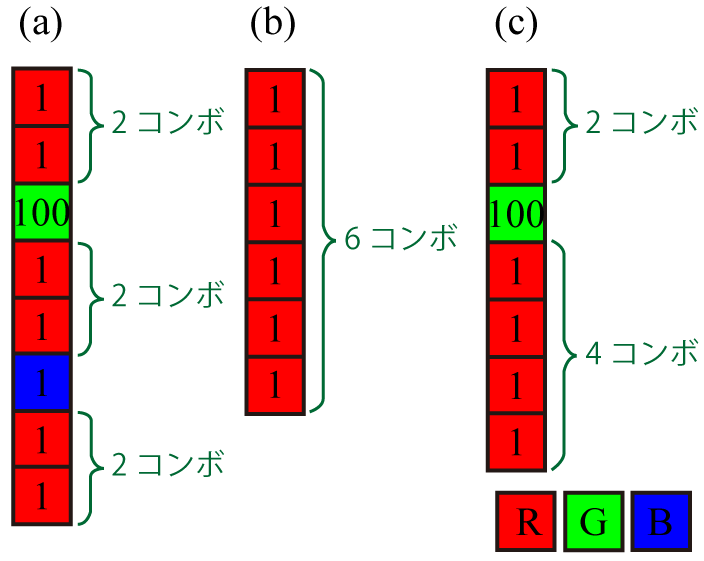  ``` 8 3 5 3 R 1 G 100 B 1 RRGRRBRR ``` 输出： ``` 126 ``` - 全部堆上去（图 (a)）：$107$ 分 + $5 \times (2-1) \times 3$ 组 + $3$ 分 $=125$ 分。 - 只堆 R（图 (b)）：$6$ 分 + $5 \times (6-1) + 0 = 31$ 分。 - 堆除 B 外的所有方块（图 (c)）：$106$ 分 + $5 \times \{(2-1)+(4-1)\} + 0 = 126$ 分。 - 所以最大得分为 $126$。 

第 $1$ 行：$n\ m\ Y\ Z$ 第 $2$ 行到第 $m+1$ 行：每行 $c_i\ p_i$ 第 $m+2$ 行：长度为 $n$ 的字符串，表示掉落方块的颜色顺序

输出能获得的最大得分，末尾换行。

- $1 \leq n \leq 5,000$ - $1 \leq m \leq 10$ - $-100 \leq Y \leq 100$ - $-10,000 \leq Z \leq 10,000$ - $-100 \leq p_i \leq 100$ - 所有输入均为整数或大写英文字母 - 不会有重复颜色 - $b_j$ 只会是 $c_1,c_2,\ldots,c_m$ 中的一种 由 ChatGPT 4.1 翻译