AT_arc010_4 [ARC010D] 情報伝播
题目描述
青木君是一名在 AtCoder 国秘密情报部工作的年轻特工,致力于情报活动。
这次,青木君接到的任务如下:
- 青木君必须将 AtCoder 国的机密信息传递给分布在二维坐标上的所有同伴。
- 但在这个二维坐标上,不仅有同伴,还混杂着敌国的间谍。
- 当青木君将机密信息传递给某个同伴后,该同伴会用扬声器扩散信息(虽然是机密信息!)。
- 用扬声器扩散信息意味着,以自己为中心,在任意半径的同心圆范围内,将信息传递给所有“人类”(包括同伴和间谍)。
- 接收到信息的同伴也会用扬声器扩散信息,信息会以此方式连锁传播。
- 当然,绝不能让间谍获得机密信息。
为完成任务,青木君只需前往每位同伴的位置,依次执行以下三步:
1. 传递机密信息;
2. 毁掉同伴手中的扬声器;
3. 再三叮嘱“不要泄露机密信息”。
但遗憾的是,青木君没有足够的时间亲自前往所有同伴的位置。
因此,青木君打算利用同伴会用扬声器扩散信息的特性,让信息高效地传递下去。
在不让间谍获知机密信息的前提下,若要让所有同伴都获得机密信息,青木君最少需要亲自传递信息给多少位同伴?
输入格式如下,通过标准输入给出。
输入格式
第 $1$ 行:一个整数 $N$,表示同伴的数量,$1 \leq N \leq 5,000$。
第 $2$ 行到第 $N+1$ 行:每行两个整数 $f_{xi}$ 和 $f_{yi}$,表示第 $i$ 个同伴的 $X$ 坐标和 $Y$ 坐标,$-10^9 \leq f_{xi}, f_{yi} \leq 10^9$。
第 $N+2$ 行:一个整数 $M$,表示间谍的数量,$0 \leq M \leq 100,000$。
第 $N+3$ 行到第 $N+M+2$ 行:每行两个整数 $s_{xj}$ 和 $s_{yj}$,表示第 $j$ 个间谍的 $X$ 坐标和 $Y$ 坐标,$-10^9 \leq s_{xj}, s_{yj} \leq 10^9$。
同一坐标上不会有多个人。
当 $M > 1,000$ 时,保证间谍是随机分布的。
仅对 $0 \leq N \leq 10$ 的输入全部答对可获得 $10$ 分。
仅对 $0 \leq N \leq 30$ 的输入全部答对可获得 $50$ 分。
输出格式
输出青木君需要亲自传递机密信息的最小同伴人数。输出到标准输出,末尾需换行。
说明/提示
```
3
1 1
1 2
2 1
0
```
```
1
```
- 只需将信息传递给坐标 $(1, 1)$ 的同伴,所有 $3$ 位同伴都能获得信息。
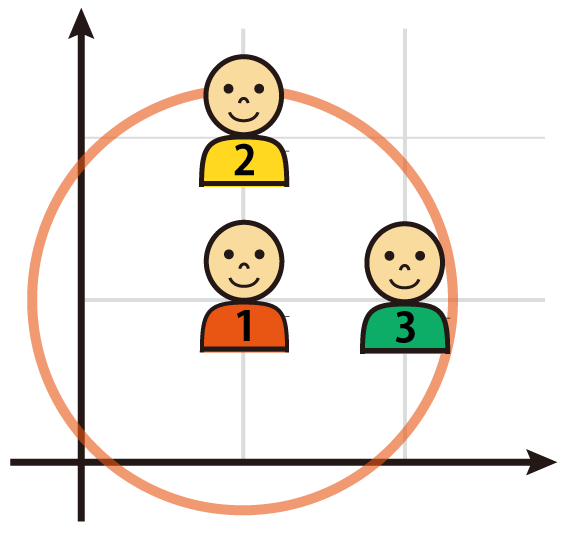
```
2
1 1
1 2
1
2 1
```
```
1
```
- 只需将信息传递给坐标 $(1, 2)$ 的同伴,所有 $2$ 位同伴都能获得信息。
- 若从 $(1, 1)$ 传递到 $(1, 2)$,必然会被间谍发现。
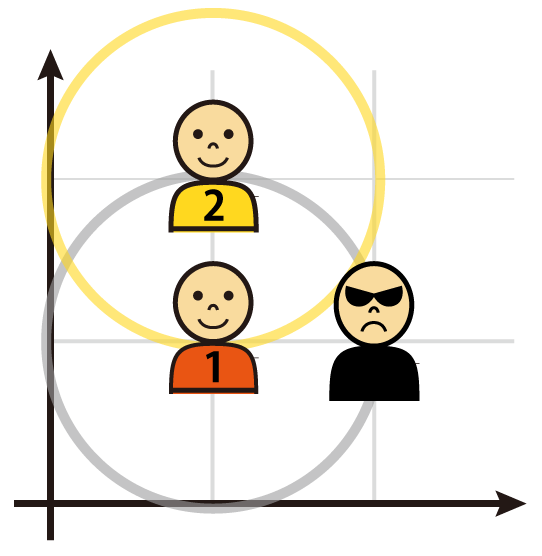
```
5
1 1
1 2
2 3
3 3
5 3
2
2 1
4 4
```
```
2
```
- 只需将信息传递给 $(2, 3)$ 的同伴,即可让 $(1, 2)$ 和 $(3, 3)$ 的同伴获得信息。
- 随后,$(1, 2)$ 的同伴可将信息传递给 $(1, 1)$ 的同伴。
- $(5, 3)$ 的同伴则需单独传递信息。
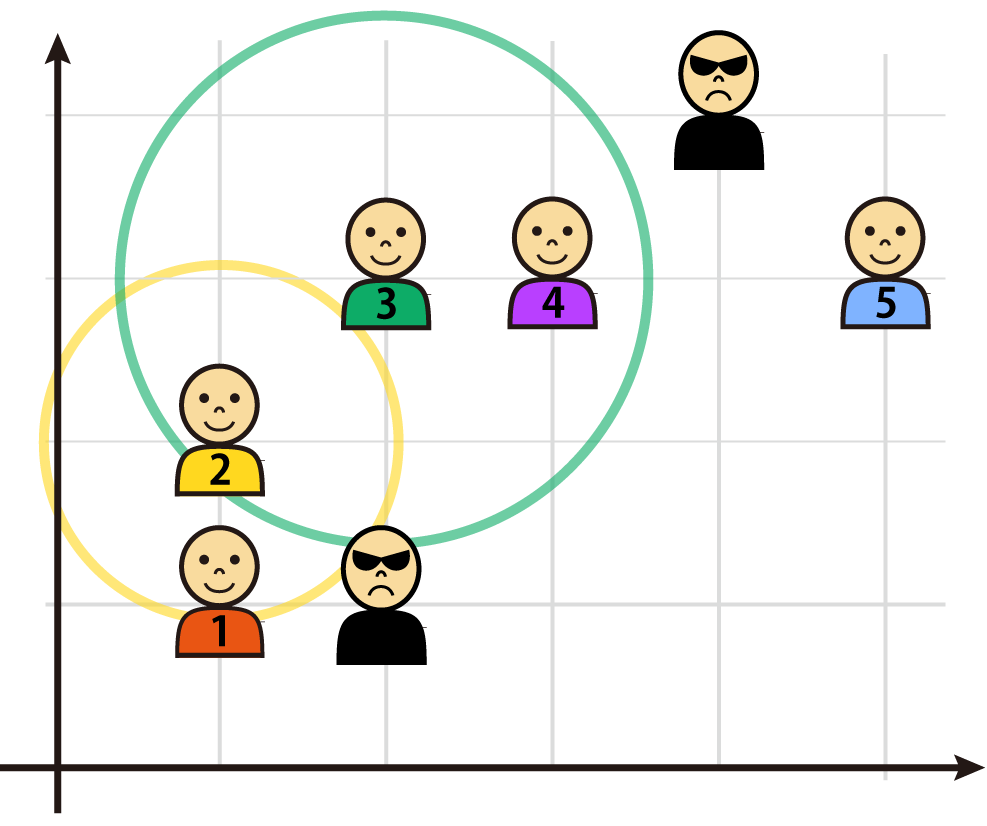
```
10
-10 5
2 9
-4 4
10 -9
8 3
5 6
4 -5
6 8
-8 10
-4 -2
10
-1 2
-2 -7
9 -3
-5 5
6 -10
-10 9
7 4
2 1
-10 1
-5 2
```
```
8
```
由 ChatGPT 4.1 翻译