AT_arc013_3 [ARC013C] 笑いをとれるかな？

[problemUrl]: https://atcoder.jp/contests/arc013/tasks/arc013_3 デビュー1年目の若手芸人「あっとこーだー」の高橋くんと青木くんは、地方ローカル番組に出演することになりました。 この番組では「ドキドキ☆ハバネロゲーム」というゲームが人気です。 以下が「ドキドキ☆ハバネロゲーム」の内容です。 1. 参加する2人はお互いに直方体の豆腐を切り取って、切り取った部分を食べます。 2. ハバネロが含まれる部分を食べたほうが負けです。 3. 高橋くんと青木くんはそれぞれ $ 1 $ 回ずつ交互に切り取ります。 4. この豆腐のある部分にはハバネロが仕掛けられています。 5. 豆腐は複数存在することがあります。 6. 全ての豆腐にハバネロが必ず仕掛けられています。 高橋くんと青木くんはリアクション芸が苦手なので、ハバネロが含まれた部分を食べてしまうと視聴者の失笑を買うことはわかっています。 そのため、この2人は相方にハバネロを食べさせることで自分がすべることを全力で回避しようと考えています。 そこで、高橋くんと青木くんは相方に知られないように番組のプロデューサからハバネロの位置をこっそりと聞き出しました。 この2人が「ドキドキ☆ハバネロゲーム」において最善手を繰り返すとき、先にハバネロを食べてすべってしまうのはどちらでしょうか。 あなたは神の視点から、この滑稽な$ 2 $人の行く末を高橋くんだけに教えることにしました。 なお、先攻は高橋くんで、豆腐の切り方は以下の通りです。 - 切り取り方は水平に $ 3 $ 方向から切り取ることができます。つまり、斜めに切ることはできません。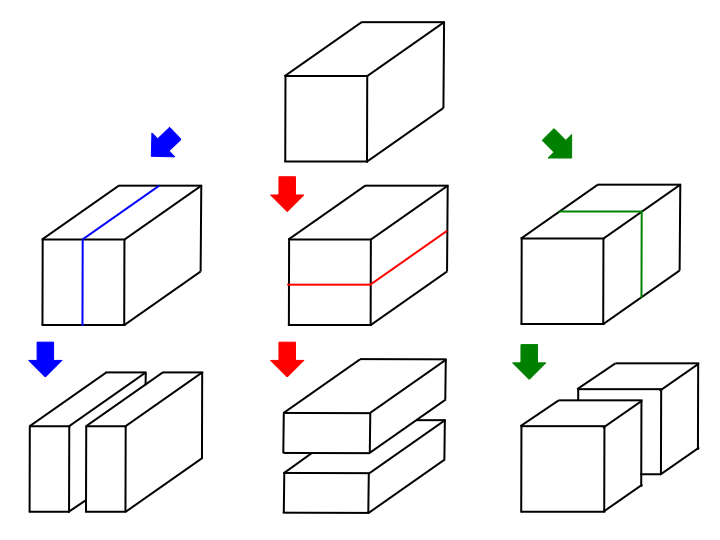 - 豆腐の1辺の長さが必ず整数になるよう切断します。 - 例として、 $ 2*2*2 $ の豆腐の切り方の一例を示します。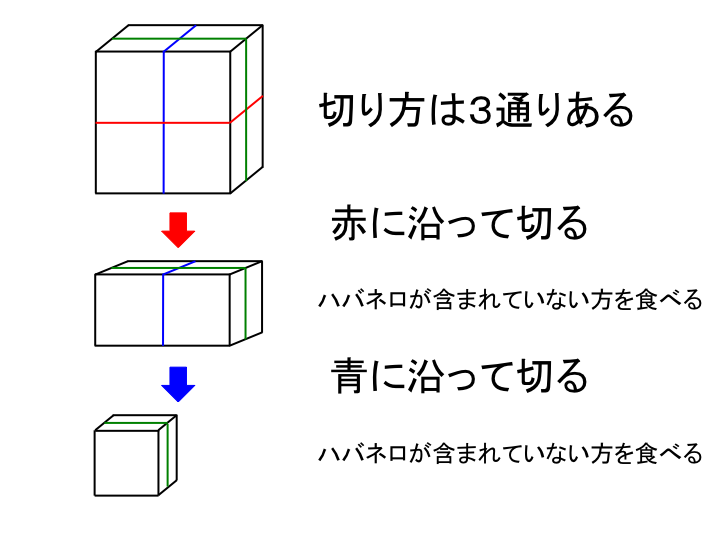  入力は以下の形式で標準入力から与えられる。 > $ N $ $ X_{1} $ $ Y_{1} $ $ Z_{1} $ $ M_{1} $ $ x_{1,0} $ $ y_{1,0} $ $ z_{1,0} $ $ x_{1,1} $ $ y_{1,1} $ $ z_{1,1} $ : $ x_{1,M_{1}-1} $ $ y_{1,M_{1}-1} $ $ z_{1,M_{1}-1} $ $ X_{2} $ $ Y_{2} $ $ Z_{2} $ $ M_{2} $ $ x_{2,0} $ $ y_{2,0} $ $ z_{2,0} $ $ x_{2,1} $ $ y_{2,1} $ $ z_{2,1} $ : $ x_{2,M_{2}-1} $ $ y_{2,M_{2}-1} $ $ z_{2,M_{2}-1} $ : $ X_{N} $ $ Y_{N} $ $ Z_{N} $ $ M_{N} $ $ x_{N,0} $ $ y_{N,0} $ $ z_{N,0} $ $ x_{N,1} $ $ y_{N,1} $ $ z_{N,1} $ : $ x_{N-1,M_{N}-1} $ $ y_{N,M_{N}-1} $ $ z_{N,M_{N}-1} $ 1. $ 1 $ 行目には豆腐の数 $ N(1≦N≦1,000) $ が与えられる。 2. 半角スペースで区切りで与えられる $ X_{i} $ $ Y_{i} $ $ Z_{i} $ は $ i $ 番目に与えられる豆腐のサイズで、 - $ X_{i} $ は $ i $ 番目の豆腐のタテの長さ。 - $ Y_{i} $ は $ i $ 番目の豆腐のヨコの長さ。 - $ Z_{i} $ は $ i $ 番目の豆腐の高さ。 - $ X_{i},Y_{i},Z_{i} $ はそれぞれ整数で、 $ 1≦X_{i},Y_{i},Z_{i}≦1,000,000,000 $ であることが保証されている。 14. $ M_{i}(1≦M_{i}≦100) $ は $ i $ 番目の豆腐に仕掛けられてたハバネロの数です。 15. そのあと、半角スペースで区切りで与えられる $ x_{i,j} $ $ y_{i,j} $ $ z_{i,j} $ において - $ x_{i,j} $ は $ i $ 番目の豆腐に仕掛けられた $ j $ 番目のハバネロの $ x $ 座標 - $ y_{i,j} $ は $ i $ 番目の豆腐に仕掛けられた $ j $ 番目のハバネロの $ y $ 座標 - $ z_{i,j} $ は $ i $ 番目の豆腐に仕掛けられた $ j $ 番目のハバネロの $ z $ 座標 - をそれぞれ示す。たとえば、座標$ (1,\ 1,\ 1) $ にハバネロが仕掛けられた場合、下図のような位置にある。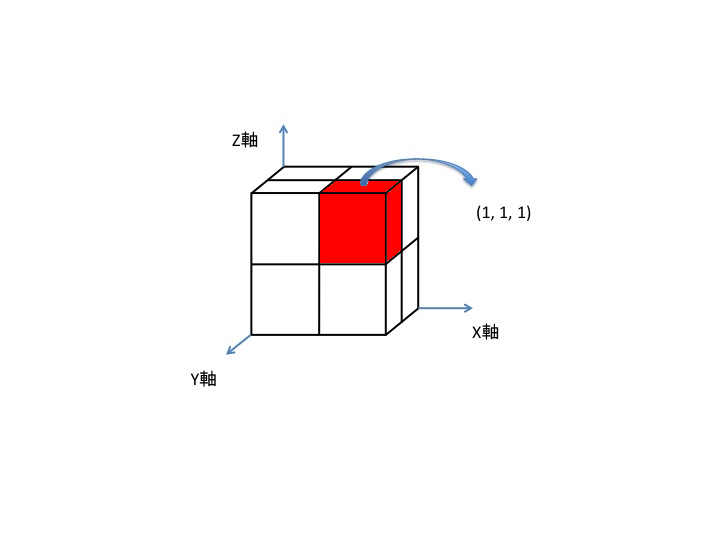  - $ N\ =\ 1 $ かつ $ 1≦X_{i},Y_{i},Z_{i}≦20 $ を満たす入力にのみ正解した場合、部分点として $ 30 $ 点が与えられる。 先攻の高橋くんが勝利する場合は`WIN`を、高橋くんが敗北する場合は`LOSE`を、それぞれ $ 1 $ 行で出力すること。 また、出力の最後には改行をいれること。 ```

1
2 3 3
1
1 1 1
```

 ```
WIN
```

- 高橋君が最初に $ x=0 $ の豆腐を食べてしまうことで、確実に勝つことができます。
 
```
1
3 3 3
1
1 1 1
```

 ```
LOSE
```

- 豆腐とハバネロの形が点対称になっているので、高橋君が食べた側と反対側の豆腐を食べられると、高橋君は絶対に勝つことができません。
 
```
2
4 4 4
1
1 1 1
4 4 4
1
2 2 2
```

 ```
LOSE
```

- 二つの豆腐は同じ形をしているので、高橋君が食べた豆腐と、反対側の豆腐を同じように食べられてしまうと、高橋君は絶対に勝つことができません。
                            

N/A

N/A