AT_arc018_4 [ARC018D] 僕は友達が少ない
Description
[problemUrl]: https://atcoder.jp/contests/arc018/tasks/arc018_4
高橋君の通う大学は、毎年 $ N $ 人の新入生を迎え入れています。 $ N $ 人の新入生には $ 1 $ から $ N $ の学籍番号が順番に振られていて、高橋君の学籍番号は $ 1 $ です。 さて、4月から大学に通う高橋君は他の $ N-1 $ 人の新入生全員と友達になりたいと思っています。しかし、それを達成するには非常に費用が掛かることが知られています。 高橋君にとって、"x君と友達である"というのは高橋君の友達の友達の...というふうに交友関係を辿って、x君にたどり着くことが可能な状態のことを指します。 現在、新入生同士はお互いを全く知らず、互いに友達であるような学生はいません。当然、高橋君にも全く友達がいません。しかし、高橋君は特定の2人の学生(高橋君も含むことがあります)について、「少なくともどちらか一方が高橋君の友達もしくは高橋君自身であるような、学籍番号が $ A $ の学生と 学籍番号が $ B $ の学生を、$ C $ 円使って友達同士にする」という形式の手段を $ M $ 種類知っています。また、学生によって必要となる費用はバラバラであるため、同じ費用である手段の数はそこまで偏っていません。 最初、高橋君を含めた新入生に友達は全くおらず、高橋君は上記の手段を活用し、新入生全員と友達になることを考えています。また、高橋君はそれ以外の方法で友達を作ることはできません。しかし、高橋君の資金力にも限りがあり、出来るだけ少ない費用で新入生全員と友達になりたいと考えています。高橋君は忙しいので、プログラマーであるあなたに、この企てについての仕事を依頼することにしました。 高橋君からあなたに与えられた仕事を説明します。 まず、あなたには、大学に在籍する高橋君を含む新入生の数 $ N $ 、手段の数 $ M $ と、 $ M $ 種類の手段の情報が与えられます。 $ N $ 人の新入生には $ 1 $ から $ N $ の学籍番号が順番に振られていて、高橋君の学籍番号は $ 1 $ です。 あなたの仕事は、高橋君が新入生全員と友達になるために必要な合計の費用と、最小限の費用を達成する手段の選び方が何通りあるかを出力することです。手段を実行する順番のみが異なるものは同じ手段の選び方とみなします。正確には、選び方の数は非常に大きくなってしまうことがあるので、選び方の数を $ 1,000,000,007 $ で割った余りを出力してください。 この問題には部分点が設定されている。
- 下記の条件を満たすテストケースのみで構成された、 $ 10 $ 点分のセットがある。
- 手段に必要な費用は全て相異なる。つまり 、 $ i,j\ (1≦i,j≦M) $ において、 $ i\ \neq\ j $ なら $ C_i\ \neq\ C_j $ が成立する。
- 上記のセットを含む全てのテストケースに正解することで、残りの $ 90 $ 点を得られる。
高橋君が新入生全員と友達となるために必要な最小の費用と、最小の費用を達成する手段の選び方の数を $ 1,000,000,007 $ で割った余りを、半角スペース区切りで一行に出力せよ。
なお、出力の最後には改行を入れること。 ```
4 4 1 2 4000 2 3 3000 3 4 2000 1 4 1000 ``` ```6000 1 ``` この入力は「手段に必要な費用は全て相異なる」という部分点( $ 10 $ 点分)の制約を満たしている。 $ 1 $ 番目~ $ 4 $ 番目の合計 $ 4 $ 種類の手段が存在する。高橋君が全ての新入生と友達になるために必要な最小費用は $ 6,000 $ 円で、それを達成する手段の組み合わせは次の $ 1 $ 通りである。 8. $ 2,3,4 $ 番目の手段を適切な順番で用いる。 具体的に、どのようにして高橋君が学生全員と友達になるのかを説明する。 1. まず最初に、高橋君には友達がいないので、高橋君(学籍番号 $ 1 $)が含まれる手段しか用いることができない。したがって、手段 $ 4 $ を使い、高橋君(学籍番号 $ 1 $)と学籍番号 $ 4 $ の学生を友達同士にする。 2. 次に、この時点で学籍番号 $ 4 $ の学生は既に高橋君の友達であるため、手段 $ 3 $ を用いることができる。したがって、手段 $ 3 $ を用いて、学籍番号 $ 3 $ の学生と学籍番号 $ 4 $ の学生を友達同士にする。 3. 最後に、手段 $ 2 $ を用いて、学籍番号 $ 2 $ の学生と学籍番号 $ 3 $ の学生を友達同士にする。 以上の順番で手段を用いれば、高橋君は $ 6,000 $ 円の費用で新入生全員と友達になることができる。 ```4 5 1 2 1000 1 3 1000 2 3 2000 2 4 1000 3 4 1000 ``` ```3000 4 ``` $ 1 $ 番目~ $ 5 $ 番目の合計 $ 5 $ 種類の手段が存在する。高橋君が全ての新入生と友達になるために必要な最小費用は $ 3,000 $ 円で、それを達成する手段の組み合わせは次の $ 4 $ 通りである。 15. $ 2,4,5 $ 番目の手段を適切な順番で用いる。 16. $ 1,4,5 $ 番目の手段を適切な順番で用いる。 17. $ 1,2,5 $ 番目の手段を適切な順番で用いる。 18. $ 2,2,4 $ 番目の手段を適切な順番で用いる。 以下の図は、入力例2と、その答えを視覚的に表したものである。新入生同士を結ぶ線が手段に対応する。 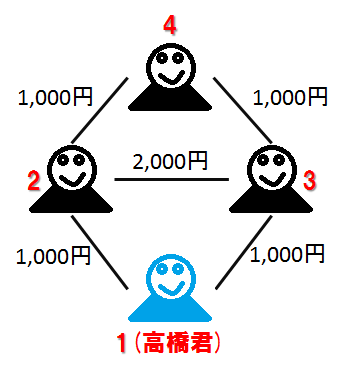 考えられる手段の選び方は、以下の $ 4 $ 通りである。 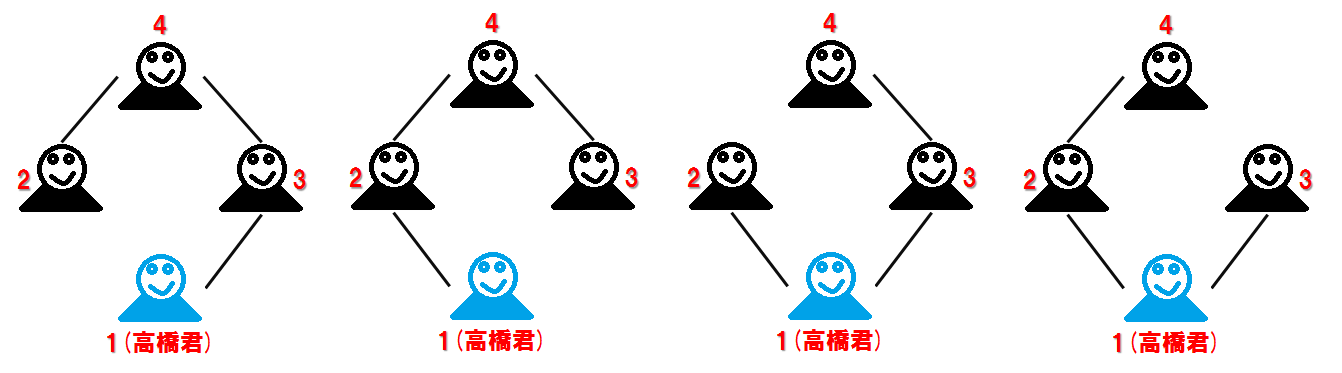 ```6 8 1 3 1 1 2 1 2 3 1 2 4 2 3 4 2 3 6 2 4 5 2 5 6 1 ``` ```7 15 ``` ```12 66 1 2 1 1 3 1 1 4 1 1 5 1 1 6 1 1 7 1 1 8 1 1 9 1 1 10 1 1 11 1 1 12 1 2 3 1 2 4 1 2 5 1 2 6 1 2 7 1 2 8 1 2 9 1 2 10 1 2 11 1 2 12 1 3 4 1 3 5 1 3 6 1 3 7 1 3 8 1 3 9 1 3 10 1 3 11 1 3 12 1 4 5 1 4 6 1 4 7 1 4 8 1 4 9 1 4 10 1 4 11 1 4 12 1 5 6 1 5 7 1 5 8 1 5 9 1 5 10 1 5 11 1 5 12 1 6 7 1 6 8 1 6 9 1 6 10 1 6 11 1 6 12 1 7 8 1 7 9 1 7 10 1 7 11 1 7 12 1 8 9 1 8 10 1 8 11 1 8 12 1 9 10 1 9 11 1 9 12 1 10 11 1 10 12 1 11 12 1 ``` ```11 917363797 ```
Input Format
N/A
Output Format
N/A
Explanation/Hint
### 部分点
入力は以下の形式で標準入力から与えられる。
> $ N M $ $ A_1 $ $ B_1 $ $ C_1 $ $ A_2 $ $ B_2 $ $ C_2 $ : $ A_M $ $ B_M $ $ C_M $
- $ 1 $ 行目には、大学に在籍する高橋君を含む新入生の数 $ N\ (2\ ≦\ N\ ≦\ 10,000) $ と、手段の数 $ M\ (1\ ≦\ M\ ≦\ 100,000) $ が与えられる。
- $ 2 $ 行目から $ M $ 行では、手段の情報が与えられる。このうち $ i\ (1\ ≦\ i\ ≦\ M) $ 行目では、$ i $ 番目の手段における 2 人の学生の学籍番号とその費用を表す 3 つの整数 $ A_i,B_i,C_i\ (1\ ≦\ A_i\ が空白区切りで与えられる。M $ 個の手段は以下の条件を満たす。
- ある学生の組を直接友達にする手段は1つ以下である。つまり、 $ i\ \neq\ j $ ならば $ (A_i,\ B_i)\ \neq\ (A_j,\ B_j) $ である。
- 任意の費用 $ K $ について、 $ (C_i\ =\ K\ であるような手段の数)\ ≦\ 100 $ が成り立つ。
- 高橋君が新入生全員と友達になる方法は必ず存在する。
この問題には部分点が設定されている。 - 下記の条件を満たすテストケースのみで構成された、 $ 10 $ 点分のセットがある。
- 手段に必要な費用は全て相異なる。つまり 、 $ i,j\ (1≦i,j≦M) $ において、 $ i\ \neq\ j $ なら $ C_i\ \neq\ C_j $ が成立する。
- 上記のセットを含む全てのテストケースに正解することで、残りの $ 90 $ 点を得られる。