AT_arc018_4 [ARC018D] 僕は友達が少ない

高桥君所在的大学每年会迎来 $N$ 名新生。新生们的学号从 $1$ 到 $N$ 依次编号，高桥君的学号为 $1$。即将于四月入学的高桥君希望能和其他 $N-1$ 名新生全部成为朋友。然而，实现这一目标需要花费大量的费用。 对于高桥君来说，“与 x 君是朋友”指的是通过朋友的朋友……这样的关系链，可以最终到达 x 君的状态。 目前，新生之间彼此完全不认识，没有任何两个人是朋友。当然，高桥君也还没有任何朋友。不过，高桥君知道 $M$ 种方式，每种方式可以让指定的两名学生（可能包括高桥君本人）成为朋友，前提是这两人中至少有一人已经是高桥君的朋友或高桥君本人。具体来说，第 $i$ 种方式可以花费 $C_i$ 日元，让学号为 $A_i$ 的学生和学号为 $B_i$ 的学生成为朋友。 由于每位学生所需的费用各不相同，因此相同费用的方式数量不会太多。 最初，包括高桥君在内的新生都没有朋友。高桥君只能利用上述方式来结交朋友，除此之外没有其他方法。由于资金有限，高桥君希望以尽可能少的费用与所有新生成为朋友。高桥君事务繁忙，因此委托你来完成这个任务。 你的任务如下： 你将获得新生总数 $N$、方式总数 $M$，以及 $M$ 种方式的详细信息。新生的学号从 $1$ 到 $N$ 编号，高桥君的学号为 $1$。 请你输出高桥君与所有新生成为朋友所需的最小总费用，以及实现最小费用的方式选择方案数。仅方式选择顺序不同的情况视为同一种选择方案。由于方案数可能非常大，请输出方案数对 $1,000,000,007$ 取模的结果。输出时，两项之间用半角空格分隔，最后输出换行符。 本题设有部分分。 - 有一组仅包含满足如下条件的测试数据，价值 $10$ 分。 - 所有方式的费用均互不相同。即对于任意 $i,j\ (1\leq i,j\leq M)$，若 $i\neq j$，则 $C_i\neq C_j$。 - 若能通过上述数据集以及所有测试数据获得正确答案，则可获得剩余 $90$ 分。 例如，输入如下： ``` 4 4 1 2 4000 2 3 3000 3 4 2000 1 4 1000 ``` 输出： ``` 6000 1 ``` 此输入满足“所有方式的费用均互不相同”的部分分（$10$ 分）限制。共有 $4$ 种方式。高桥君与所有新生成为朋友所需的最小费用为 $6,000$ 日元，实现该费用的方式选择方案有 $1$ 种。具体操作如下： 1. 最初高桥君没有朋友，因此只能使用包含高桥君（学号 $1$）的方式。于是使用第 $4$ 种方式，让高桥君（学号 $1$）和学号 $4$ 的学生成为朋友。 2. 此时学号 $4$ 的学生已是高桥君的朋友，可以使用第 $3$ 种方式，让学号 $3$ 和学号 $4$ 的学生成为朋友。 3. 最后使用第 $2$ 种方式，让学号 $2$ 和学号 $3$ 的学生成为朋友。 按照上述顺序操作，高桥君可以用 $6,000$ 日元与所有新生成为朋友。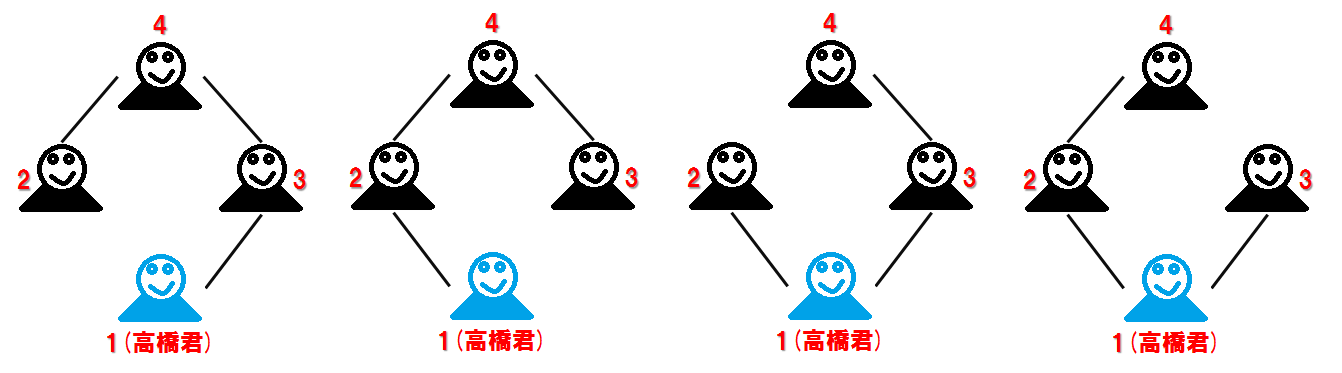 再如，输入如下： ``` 4 5 1 2 1000 1 3 1000 2 3 2000 2 4 1000 3 4 1000 ``` 输出： ``` 3000 4 ``` 共有 $5$ 种方式。高桥君与所有新生成为朋友所需的最小费用为 $3,000$ 日元，实现该费用的方式选择方案有 $4$ 种。具体方案如下： 1. 选择第 $2,4,5$ 种方式的某种顺序。 2. 选择第 $1,4,5$ 种方式的某种顺序。 3. 选择第 $1,2,5$ 种方式的某种顺序。 4. 选择第 $2,2,4$ 种方式的某种顺序。 下图展示了输入样例 2 及其答案的可视化。连接新生的线条对应于方式。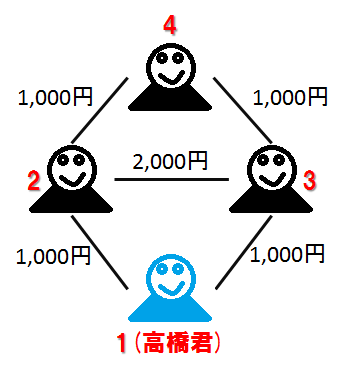  可行的方式选择方案如下：  再如，输入如下： ``` 6 8 1 3 1 1 2 1 2 3 1 2 4 2 3 4 2 3 6 2 4 5 2 5 6 1 ``` 输出： ``` 7 15 ``` 再如，输入如下： ``` 12 66 1 2 1 1 3 1 1 4 1 1 5 1 1 6 1 1 7 1 1 8 1 1 9 1 1 10 1 1 11 1 1 12 1 2 3 1 2 4 1 2 5 1 2 6 1 2 7 1 2 8 1 2 9 1 2 10 1 2 11 1 2 12 1 3 4 1 3 5 1 3 6 1 3 7 1 3 8 1 3 9 1 3 10 1 3 11 1 3 12 1 4 5 1 4 6 1 4 7 1 4 8 1 4 9 1 4 10 1 4 11 1 4 12 1 5 6 1 5 7 1 5 8 1 5 9 1 5 10 1 5 11 1 5 12 1 6 7 1 6 8 1 6 9 1 6 10 1 6 11 1 6 12 1 7 8 1 7 9 1 7 10 1 7 11 1 7 12 1 8 9 1 8 10 1 8 11 1 8 12 1 9 10 1 9 11 1 9 12 1 10 11 1 10 12 1 11 12 1 ``` 输出： ``` 11 917363797 ```

输入通过标准输入给出，格式如下： > $N\ M$ > $A_1\ B_1\ C_1$ > $A_2\ B_2\ C_2$ > $\vdots$ > $A_M\ B_M\ C_M$ - 第 $1$ 行包含两个整数，分别表示新生总数 $N\ (2\leq N\leq 10,000)$ 和方式总数 $M\ (1\leq M\leq 100,000)$。 - 接下来 $M$ 行，每行包含三个整数 $A_i,\ B_i,\ C_i\ (1\leq A_i,B_i\leq N,\ 1\leq C_i\leq 10^9)$，表示第 $i$ 种方式的两名学生学号及所需费用。方式之间以空格分隔。 - 对于任意 $i\neq j$，$(A_i,B_i)\neq (A_j,B_j)$。 - 对于任意费用 $K$，费用为 $K$ 的方式数量不超过 $100$。 - 一定存在使高桥君与所有新生成为朋友的方法。 本题设有部分分。 - 有一组仅包含满足如下条件的测试数据，价值 $10$ 分。 - 所有方式的费用均互不相同。即对于任意 $i,j\ (1\leq i,j\leq M)$，若 $i\neq j$，则 $C_i\neq C_j$。 - 若能通过上述数据集以及所有测试数据获得正确答案，则可获得剩余 $90$ 分。

输出一行，包含两个整数，分别表示高桥君与所有新生成为朋友所需的最小总费用，以及实现最小费用的方式选择方案数。两项之间用半角空格分隔，最后输出换行符。方案数需对 $1,000,000,007$ 取模。

### 部分分 - 有一组仅包含满足如下条件的测试数据，价值 $10$ 分。 - 所有方式的费用均互不相同。即对于任意 $i,j\ (1\leq i,j\leq M)$，若 $i\neq j$，则 $C_i\neq C_j$。 - 若能通过上述数据集以及所有测试数据获得正确答案，则可获得剩余 $90$ 分。 由 ChatGPT 4.1 翻译