AT_arc030_1 [ARC030A] 閉路グラフ
题目描述
如下图所示,有由$n(n≥3)$顶点构成的闭路图表。
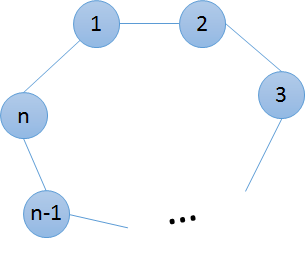
该图表连接顶点$1$和顶点$2$的边,顶点$2$和顶点$3$…由连接顶点$n-1$和顶点$n$,以及顶点$n$和顶点$1$的边构成。
你想通过从这个图表中去除几个顶点来分割图表,最终做成只剩下$k$个连接成分的图表。在实际开始去除顶点之前,请判断这样的去除方法是否存在。
去除某个顶点的话,与该顶点直接相连的边也会被去除。另外,如果不需要的话,不去除$1$的顶点也没关系。
输入格式
输入以以下形式从标准输入被给予。
> $ n $ $ k $
------------
- 在第$1$行中,给出表示闭路图表顶点数的整数$n(3≤n≤10^5)$。
- 在第$2$行中,给出表示想要保留的连接成分的数量的整数$k(1≤k≤10^5)$。
输出格式
第1行,$n $ 从顶点的闭路图表中去掉几个顶点,如果正好可以做成含有$k$个连接成分的图表输出`YES`,否则输出`NO`,最后不要忘记换行。
说明/提示
例如,如下图所示,通过去除顶点$1$和顶点$3$,正好可以留下$2$个连接成分。
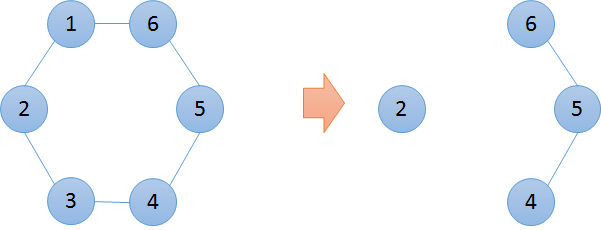
输入的图表如下图所示,无论怎样去除顶点,都不能只留下$2$个连接成分。
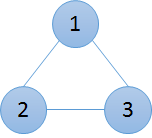
Translated by [xiaoZTD](https://www.luogu.com.cn/user/1541004)