AT_arc037_d [ARC037D] Chaotic Polygons

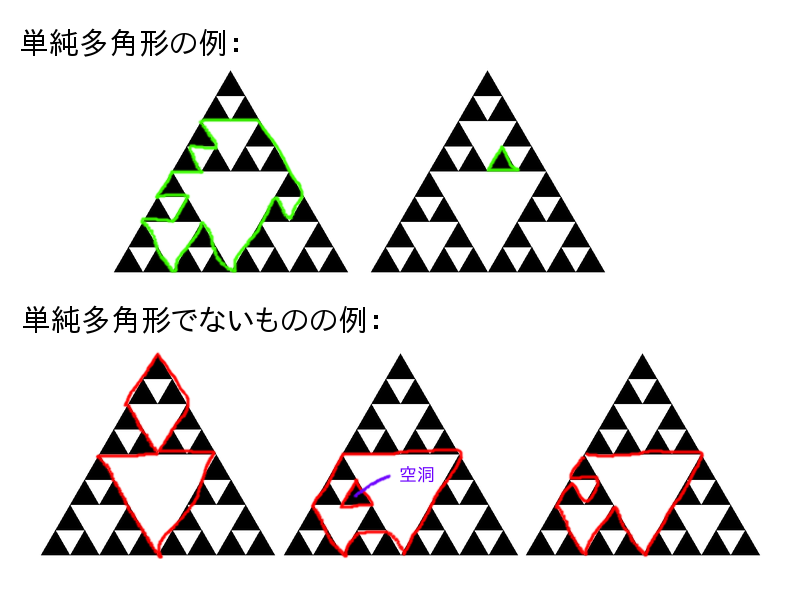
对于非负整数 $L$，$L$ 级的谢尔宾斯基垫片定义如下： - $0$ 级的谢尔宾斯基垫片是一个正三角形。 - $i$ 级（$i \geq 1$）的谢尔宾斯基垫片，是对 $i-1$ 级谢尔宾斯基垫片中包含的 $3i-1$ 个正三角形分别进行如下操作后得到的图形： （操作）连接正三角形每条边的中点，在中心形成一个较小的正三角形。将该正三角形从图形中移除（这样，原来的正三角形被分割成 $3$ 个较小的正三角形）。 下图展示了 $0,1,2,3,4$ 级的谢尔宾斯基垫片。  给定正整数 $L$。考虑 $L$ 级谢尔宾斯基垫片中包含的 $3L$ 个正三角形的所有边。请计算由这些线段组成的所有简单多边形（即没有自交的多边形）的个数，并将结果对 $1,000,000,007$ 取模后输出。即使是相似的多边形，只要位置不同也要区分。 下图给出了需要计数的多边形和不需要计数的多边形的例子。 

输入从标准输入按以下格式给出。 > $L$ - 第 $1$ 行给出整数 $L$，$1 \leq L \leq 10^5$。

输出所求多边形的个数对 $1,000,000,007$ 取模的结果，并以换行符结尾。

### 样例解释 1 存在如下 $11$ 个简单多边形。  由 ChatGPT 4.1 翻译