AT_arc037_d [ARC037D] Chaotic Polygons
Description
[problemUrl]: https://atcoder.jp/contests/arc037/tasks/arc037_d
非負整数 $ L $ に対し、レベル $ L $ のシェルピンスキーのガスケットとは次のような図形である。
- レベル $ 0 $ のシェルピンスキーのガスケットとは、 $ 1 $ 個の正三角形である。
- レベル $ i $ ($ i $ $ ≧ $ $ 1 $) のシェルピンスキーのガスケットは、レベル $ i-1 $ のシェルピンスキーのガスケットに含まれる $ 3i-1 $ 個の正三角形それぞれに対して以下の操作を行って得られる図形である。
(操作) 正三角形の各辺の中点を結び、中心に小さな正三角形を作る。この正三角形を図形から取り除く(この結果、もとの正三角形は $ 3 $ つの小さな正三角形に分割される)。
以下にレベル $ 0,1,2,3,4 $ のシェルピンスキーのガスケットを図示する。

正整数 $ L $ が与えられる。レベル $ L $ のシェルピンスキーのガスケットに含まれる $ 3L $ 個の正三角形のすべての辺を考える。これらの線分から形成される単純多角形 (自己交差しない多角形) の個数を $ 1,000,000,007 $ で割った余りを求めよ。相似な多角形であっても位置が異なるものは区別する。
以下に数えるべき多角形とそうでないものの例を示す。
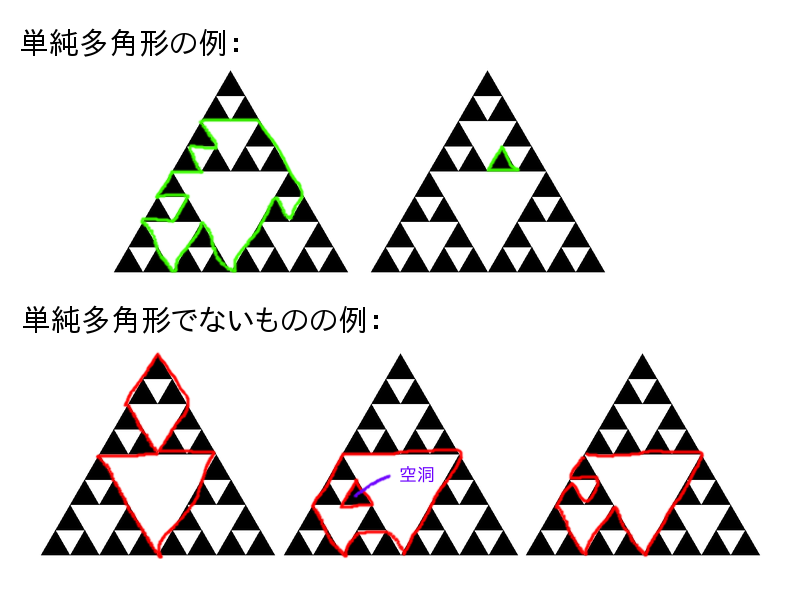
Input Format
入力は以下の形式で標準入力から与えられる。
> $ L $
- $ 1 $ 行目に、 整数 $ L $ ($ 1 $ $ ≦ $ $ L $ $ ≦ $ $ 105 $) が与えられる。
Output Format
標準出力に求める多角形の個数を $ 1,000,000,007 $ で割った余りを出力し、末尾で改行せよ。
Explanation/Hint
### Sample Explanation 1
以下の $ 11 $ 個の単純多角形が存在する。 !\[\](http://arc037.contest.atcoder.jp/img/arc/037/ljlefijfewkjfwefk/D\_sample1.png)