AT_arc062_c [ARC062E] AtCoDeerくんと立方体づくり
题目描述
[problemUrl]: https://atcoder.jp/contests/arc062/tasks/arc062_c
小鹿 AtCoDeer 君有 $N$ 块正方形瓷砖。每块正方形的一面写有 $1$ 到 $N$ 的数字,并且正方形的每个顶点都涂有颜色。颜色用 $0$ 到 $999$ 的整数表示,编号为 $i$ 的正方形,其顶点的颜色按照数字面朝上的方向,从左上、右上、右下、左下的顺序,分别为 $C_{i,0}, C_{i,1}, C_{i,2}, C_{i,3}$(参见图 $1$)。
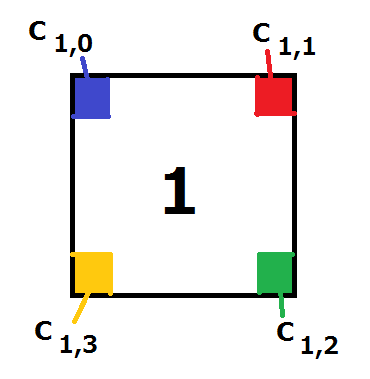
图 $1$:瓷砖的颜色与输入的对应关系
AtCoDeer 君想用这 $N$ 块瓷砖中的 $6$ 块,组合成一个满足以下条件的立方体:
- 数字面朝外。
- 对于立方体的每一个顶点,聚集在该顶点的 $3$ 个正方形的顶点颜色必须完全相同。
请你帮 AtCoDeer 君计算,满足条件的立方体有多少种不同的组合方式。需要注意的是,虽然瓷砖的颜色可能相同,但只要所用瓷砖编号不同,或者瓷砖的朝向(每块瓷砖可以通过 $90^\circ$ 旋转有 $4$ 种朝向)不同,就视为不同的立方体组合。但如果通过三维空间旋转后,所用瓷砖及其朝向完全一致,则视为同一种立方体。
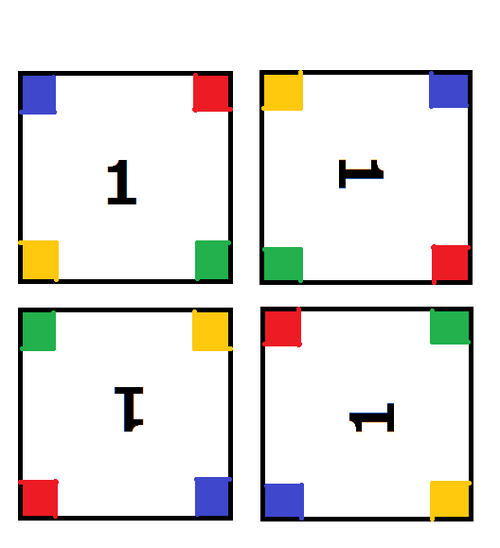
图 $2$:瓷砖的四种朝向
输入格式
输入通过标准输入给出,格式如下:
> $N$ $C_{1,0}$ $C_{1,1}$ $C_{1,2}$ $C_{1,3}$ $C_{2,0}$ $C_{2,1}$ $C_{2,2}$ $C_{2,3}$ $\cdots$ $C_{N,0}$ $C_{N,1}$ $C_{N,2}$ $C_{N,3}$
输出格式
输出 AtCoDeer 君能够制作的满足条件的立方体的组合数。
说明/提示
### 数据范围
- $6 \leq N \leq 400$
- $0 \leq C_{i,j} \leq 999\ (1 \leq i \leq N,\ 0 \leq j \leq 3)$
### 样例解释 1
可以制作如下图所示的立方体。
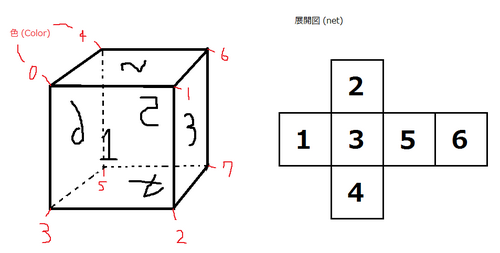
由 ChatGPT 4.1 翻译