AT_arc062_c [ARC062E] AtCoDeerくんと立方体づくり

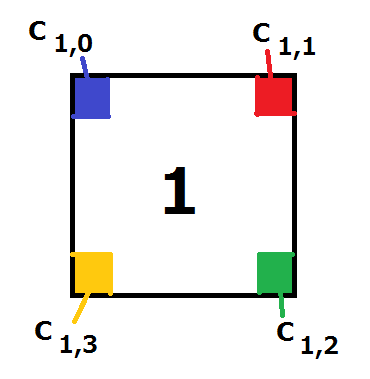[problemUrl]: https://atcoder.jp/contests/arc062/tasks/arc062_c シカのAtCoDeerくんは正方形のタイルを $ N $ 枚持っています。 各正方形の片面には $ 1～N $ の数が書いてあって、正方形の各頂点にはそれぞれ色が塗られています。色は $ 0～999 $の整数で表され、 $ i $ と書かれた正方形に塗られている色は、数の書かれている方向から見て左上、右上、右下、左下 の順に、 $ C_{i,0},C_{i,1},C_{i,2},C_{i,3} $ で与えられます(図$ 1 $を参照)。 図$ 1 $: タイルの色と入力の対応 AtCoDeerくんはこれらのタイルを$ 6 $枚組み合わせて次のような条件を満たす立方体を作ろうと考えました。 - 数の書いてある面が外側を向いている - 立方体の各頂点に対し、そこに集まる正方形の頂点は$ 3 $つあるが、それらには全て同じ色が塗られている AtCoDeerくんのために条件を満たす立方体が何通りあるか求めてください。ただし、正方形には数が書いてあるので、色の構成が同じだとしても使ったタイルが異なったり、使ったタイルの向き($ 90° $回転により$ 4 $通り考えられる)が異なるものは異なる立方体とみなします。 ただし、3次元空間で回転させることで使ったタイルの向きまで完全に一致するものは同じ立方体とみなします。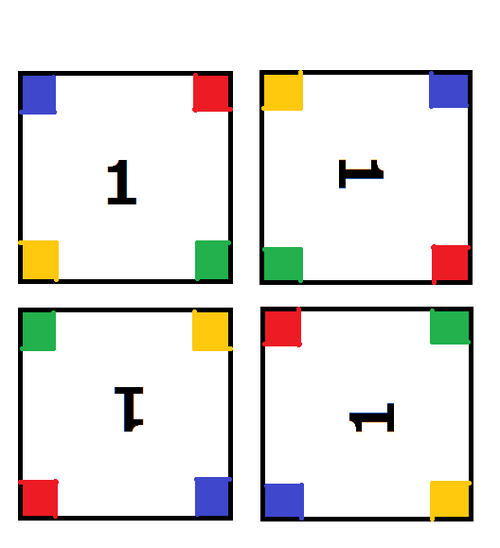 図$ 2 $: 4方向のタイルの向き

入力は以下の形式で標準入力から与えられる。 > $ N $ $ C_{1,0} $ $ C_{1,1} $ $ C_{1,2} $ $ C_{1,3} $ $ C_{2,0} $ $ C_{2,1} $ $ C_{2,2} $ $ C_{2,3} $ $ : $ $ C_{N,0} $ $ C_{N,1} $ $ C_{N,2} $ $ C_{N,3} $

AtCoDeerくんが作れる立方体が何通りあるか出力せよ。

### 制約 - $ 6≦N≦400 $ - $ 0≦C_{i,j}≦999\ (1≦i≦N\ ,\ 0≦j≦3) $ ### Sample Explanation 1 下図のような立方体が作れます。 !\[\](https://atcoder.jp/img/arc062/094fbca5395bfaaea28c98c51230693b.png)