AT_arc063_c [ARC063E] 木と整数
题目描述
有一棵包含 $N$ 个顶点的树,顶点编号为 $1, 2, \ldots, N$。第 $i$ 条边($1 \leq i \leq N-1$)连接了顶点 $A_i$ 和顶点 $B_i$。
高桥君在树上的 $K$ 个顶点上写下了整数。具体来说,对于每个 $1 \leq j \leq K$,他在顶点 $V_j$ 上写下了整数 $P_j$。之后,高桥君开始打瞌睡了。
青木君发现了这棵树,他想在剩下的所有顶点上写下整数,以此来让高桥君吃惊。要让高桥君吃惊,树需要满足以下条件:
- 条件:对于每一条边直接相连的两个顶点,它们上面写的整数之差恰好为 $1$。
请判断是否可以通过巧妙地在剩余顶点上写下整数,使得整棵树满足上述条件。如果可以,请给出一种具体的写法。
输入格式
输入以如下格式从标准输入读入。
> $N$ $A_1$ $B_1$ $A_2$ $B_2$ $\ldots$ $A_{N-1}$ $B_{N-1}$ $K$ $V_1$ $P_1$ $V_2$ $P_2$ $\ldots$ $V_K$ $P_K$
输出格式
如果可以通过在剩余顶点上写下整数使得树满足条件,则输出 `Yes`,否则输出 `No`。
如果满足条件,还需额外输出 $N$ 行。第 $v$ 行($1 \leq v \leq N$)输出写在顶点 $v$ 上的整数。若存在多种满足条件的写法,输出其中任意一种即可。
说明/提示
### 限制条件
- $1 \leq N \leq 10^5$
- $1 \leq K \leq N$
- $1 \leq A_i, B_i \leq N$($1 \leq i \leq N-1$)
- $1 \leq V_j \leq N$($1 \leq j \leq K$)(21:18,对限制条件的误记进行了修正)
- $0 \leq P_j \leq 10^6$($1 \leq j \leq K$)
- 保证给定的图一定是一棵树
- $V_j$ 互不相同
### 样例解释 1
最初,树的状态如下图所示。顶点旁边的数字表示顶点编号,顶点内部的蓝色数字表示原本写下的整数。
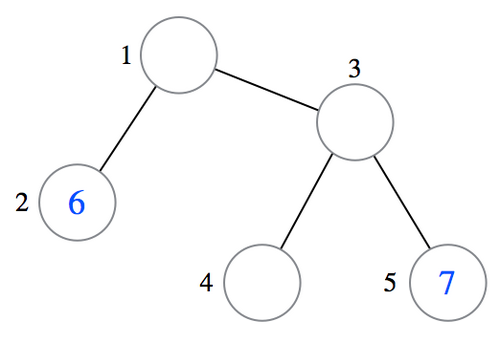
例如,青木君可以如下图所示,在剩余顶点上写下整数,使得树满足条件。这对应于输出样例 1。
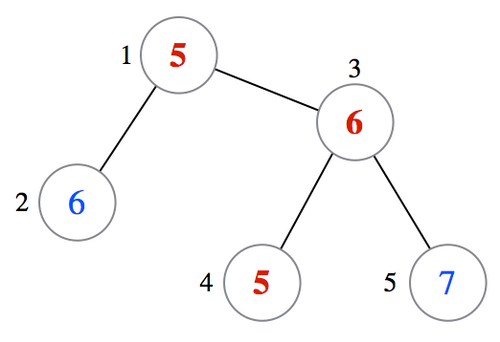
注意,只要树满足条件,输出与此不同的答案也可以。例如,对于输入样例 1,输出如下也可以:
```
Yes
7
6
8
7
7
```
### 样例解释 3
新写下的整数可以为负数,也可以超过 $10^6$。
由 ChatGPT 4.1 翻译