AT_arc082_c [ARC082E] ConvexScore

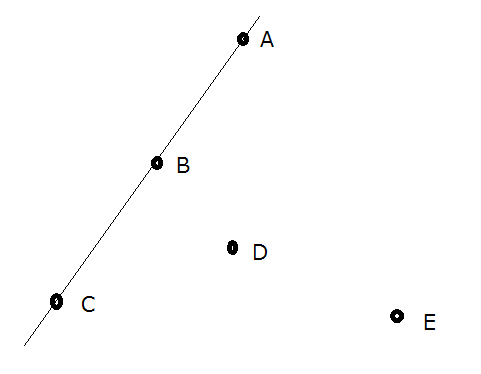
给你 $N$ 个二维平面上的点 $(x_i,y_i)$，考虑 $N$ 个点的一个子集 $S$，我们称它构成一个凸多边形，当且仅当存在一个面积为正数的凸多边形，其点集为 $S$。这个多边形的所有内角都要严格小于 $180\degree$。  例如，在上图中，$\{A,C,E\}$ 和 $\{B,D,E\}$ 构成凸多边形，$\{A,C,D,E\},{A,B,C,E},\{A,B,C\},\{D,E\}$ 和 $\{\}$ 则不构成。 对于一个点集 $S$，令 $n$ 为 $N$ 个点中位于 $S$ 的凸包内（包括内部和边界）的点的个数。我们定义 $S$ 的分数为 $2^{n-\vert S\vert}$。 求这 $N$ 个点的构成凸多边形的子集 $S$ 的分数之和。 由于答案可以很大，你需要输出答案对 $998244353$ 取模后的值。

第一行一个整数 $N(1\le N\le 200)$。 接下来 $N$ 行，每行两个整数 $x_i,y_i(0\le x_i,y_i

输出一行一个整数，表示分数之和对 $998244353$ 取模后的值。

**样例 1 解释** 我们有 $5$ 个可以构成凸多边形的 $S$，其中四个构成三角形，一个构成四边形。其中每一个的分数都是 $2^0=1$，所以答案是 $5$。 **样例 2 解释** 我们有三个 $1$ 分的三角形 $S$，两个 $2$ 分的三角形 $S$，一个 $4$ 分的三角形 $S$，所以答案是 $11$。 **样例 3 解释** 没有构成凸多边形的 $S$，所以答案是 $0$。