AT_arc164_b [ARC164B] Switching Travel

有一个包含 $N$ 个顶点的简单连通无向图，顶点编号为 $1$ 到 $N$。该图有 $M$ 条边，第 $i$ 条边连接顶点 $a_i$ 和 $b_i$。 此外，每个顶点都有白色或黑色两种颜色，初始状态由 $c_i$ 给出。若 $c_i=0$，则顶点 $i$ 初始为白色；若 $c_i=1$，则顶点 $i$ 初始为黑色。 你可以在图上任选一个顶点作为出发点，并进行如下操作任意次： - 从当前所在顶点出发，移动到与当前顶点通过边直接相连且颜色不同的顶点。移动后，出发的顶点颜色会反转（白变黑，黑变白）。 请判断，是否存在一种方案，使得经过至少一次操作后能够回到出发点。

输入通过标准输入按以下格式给出。 > $N$ $M$ > $a_1$ $b_1$ > $a_2$ $b_2$ > $\vdots$ > $a_M$ $b_M$ > $c_1$ $c_2$ $\ldots$ $c_N$

如果存在经过至少一次操作后能够回到出发点的方案，输出 `Yes`；否则输出 `No`。

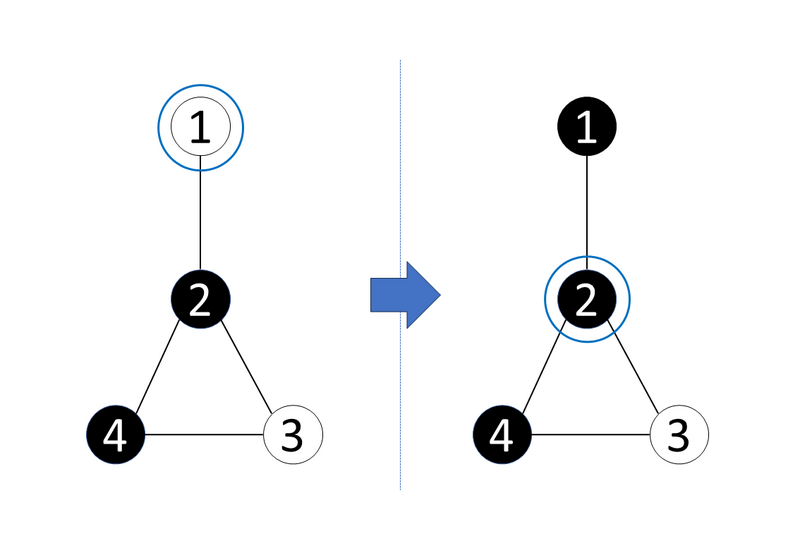
## 限制条件 - $2 \leq N \leq 2 \times 10^5$ - $N-1 \leq M \leq \min\{2 \times 10^5, N(N-1)/2\}$ - $1 \leq a_i, b_i \leq N$ $(1 \leq i \leq M)$ - $c_i=0$ 或 $c_i=1$ $(1 \leq i \leq N)$ - 给定的图是简单且连通的 - 所有输入均为整数 ## 样例解释 1 例如，考虑从顶点 $1$ 出发。第一次操作可以移动到顶点 $2$，并将出发点（顶点 $1$）的颜色由白变黑。此时的图变化如下图所示（用圆圈表示当前所在顶点）。随后依次移动到顶点 $3$、$4$、$2$，此时顶点 $1,2,3,4$ 的颜色依次为黑、白、黑、白。因此，下一步可以移动回顶点 $1$，实现回到出发点。  ## 样例解释 2 在这个图中，无论选择哪个顶点作为出发点，都无法通过满足条件的移动回到出发点。 由 ChatGPT 4.1 翻译