AT_arc177_c [ARC177C] Routing
题目描述
有一个 $N$ 行 $N$ 列(用 $(i, j)$ 表示矩阵第 $i$ 行第 $j$ 列的元素)的矩阵被刷满了红色和蓝色。现在要矩阵的一些格子刷上紫色,使得矩阵**同时**满足以下两个条件:
- 从 $(1, 1)$ 走到 $(N, N)$,保证存在一条路径使其只经过红色和紫色;
- 从 $(1, N)$ 走到 $(N, 1)$,保证存在一条路径使其只经过蓝色和紫色
注意,**行动时他可以往任何一个方向前进。**
那么,问题来了,至少要将多少格子刷成紫色才能使以上两个条件成立呢?
输入格式
输入共 $N+1$ 行。
第一行,读入 $N$;
接下来 $N$ 行,读入这个矩阵。其中以 `R` 代表红色,以 `B` 代表蓝色。
输出格式
输出仅一行,为最少刷成紫色的格子数。
**【约定】**
- $ 3\ \leq\ N\ \leq\ 500 $;
- 保证任意一个格子一定为 `R` 或 `B` 中的一个;
- 保证 $(1, 1)$ 和 $(N, N)$ 为红色;
- 保证 $(1, N)$ 和 $(N, 1)$ 为蓝色;
- 保证 $N$ 是一个整数。
**【样例解释】**
【样例 $1$ 解释】
如下图,将 $ (1, 3),(3, 2),(4, 5) $ 三个格子刷成紫色可以达成目标。
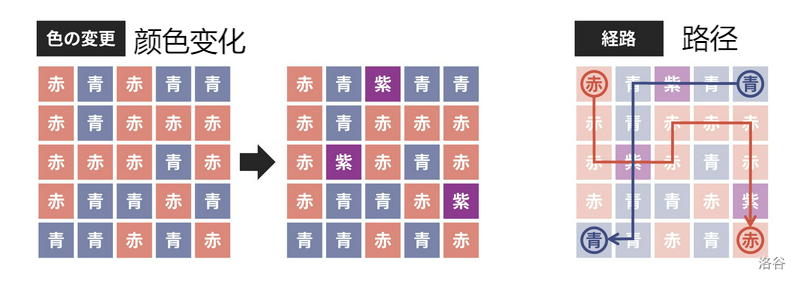
【样例 $2$ 解释】
如下图,将 $ (1, 2), (2, 2), (2, 3), (3, 3), (3, 4), (4, 4), (4, 5) $ 这 $7$ 个格子刷成紫色可以达成目标。
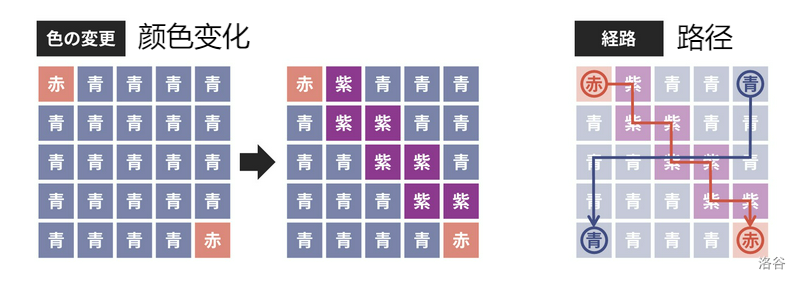
说明/提示
### 制約
- $ 3\ \leq\ N\ \leq\ 500 $
- $ c_{i,j} $ は `R` または `B`
- $ c_{1,1} $ および $ c_{N,N} $ は `R`
- $ c_{1,N} $ および $ c_{N,1} $ は `B`
- $ N $ は整数
### Sample Explanation 1
以下の図のように、マス $ (1,\ 3),\ (3,\ 2),\ (4,\ 5) $ の $ 3 $ 個を紫色に変えると、条件を満たすようになります。 !\[ \](https://img.atcoder.jp/arc177/5840bc0619592bb932aa786dc7c70dd8.png)
### Sample Explanation 2
以下の図のように、マス $ (1,\ 2),\ (2,\ 2),\ (2,\ 3),\ (3,\ 3),\ (3,\ 4),\ (4,\ 4),\ (4,\ 5) $ の $ 7 $ 個を紫色に変えると、条件を満たすようになります。 !\[ \](https://img.atcoder.jp/arc177/5191d760229aade1ae78a619d7282a65.png)