AT_arc177_d [ARC177D] Earthquakes

AtCoder 街道是一条在平坦地面上延伸的数轴直线。在这条道路上竖立着 $N$ 根高度为 $H$ 的电线杆。电线杆按照建造顺序依次编号为 $1, 2, \dots, N$。第 $i$ 根电线杆（$1 \leq i \leq N$）垂直于地面，底部固定在坐标 $X_i$ 处。**电线杆的最下端固定在地面上。**这里假设电线杆足够细，可以忽略其宽度。 在 AtCoder 街道上，将会发生 $N$ 次地震。第 $i$ 次地震（$1 \leq i \leq N$）时，会发生以下事件： 1. 如果第 $i$ 根电线杆尚未倒下，则它会以 $\frac{1}{2}$ 的概率向数轴的左侧倒下，或以 $\frac{1}{2}$ 的概率向右侧倒下。 2. 如果正在倒下的电线杆碰到了尚未倒下的其他电线杆（包括碰到其底部的情况），那么被碰到的电线杆也会朝同一方向倒下。这种情况可能会连锁发生。 需要注意的是，在步骤 1 中，电线杆倒向哪一侧与其他电线杆的倒向无关。 下图展示了一次地震中电线杆倒下的一个例子。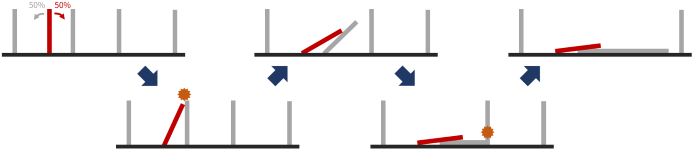  为了防震，请你对于 $t = 1, 2, \dots, N$，分别求出恰好在第 $t$ 次地震时所有电线杆全部倒下的概率，乘以 $2^N$ 后对 $998244353$ 取模的结果。可以证明，输出的结果一定是整数。

输入以如下格式从标准输入读入： > $N$ $H$ $X_1$ $X_2$ $\cdots$ $X_N$

请按顺序输出 $t = 1, 2, \dots, N$ 时的答案，用空格分隔。

### 数据范围 - $1 \leq N \leq 2 \times 10^5$ - $1 \leq H \leq 10^9$ - $0 \leq X_i \leq 10^9\ (1 \leq i \leq N)$ - $X_1, X_2, \dots, X_N$ 互不相同 - 输入均为整数 ### 样例解释 1 下图展示了本样例输入下电线杆倒下的所有可能情况，图中分数表示达到该状态的概率。  因此，恰好在第 $1, 2, 3$ 次地震时所有电线杆全部倒下的概率分别为 $\frac{1}{2},\ \frac{1}{4},\ \frac{1}{4}$。乘以 $8$ 后，输出 $4, 2, 2$。 ### 样例解释 2 下图展示了本样例输入下电线杆倒下的所有可能情况，图中分数表示达到该状态的概率。  因此，恰好在第 $1, 2, 3, 4$ 次地震时所有电线杆全部倒下的概率分别为 $0, \frac{1}{4}, \frac{1}{4}, \frac{1}{2}$。乘以 $16$ 后，输出 $0, 4, 4, 8$。 ### 样例解释 3 恰好在第 $1, 2, 3, 4, 5, 6, 7, 8$ 次地震时所有电线杆全部倒下的概率分别为 $0, \frac{1}{4}, \frac{1}{8}, \frac{3}{16}, \frac{3}{32}, \frac{7}{64}, \frac{7}{64}, \frac{1}{8}$。 ### 样例解释 4 在第 $37$ 次地震前，不可能全部电线杆都倒下。恰好在第 $38, 39, 40$ 次地震时所有电线杆全部倒下的概率分别为 $\frac{3}{8}, \frac{3}{8}, \frac{1}{4}$。 由 ChatGPT 4.1 翻译