AT_arc177_d [ARC177D] Earthquakes

[problemUrl]: https://atcoder.jp/contests/arc177/tasks/arc177_d AtCoder 街道は、平らな地面の上に伸びる数直線で表される道路です。この道路上に $ N $ 個の高さ $ H $ の電柱が立っています。電柱には $ 1,\ 2,\ \dots,\ N $ の番号が古い順に付けられています。電柱 $ i\ (1\ \leq\ i\ \leq\ N) $ は座標 $ X_i $ に地面と垂直に立っています。**電柱の最下部は地面に固定されています。**ここで、電柱は十分に細いものとして考えます。 AtCoder 街道ではこれから $ N $ 回の地震が発生します。$ i $ 回目 $ (1\ \leq\ i\ \leq\ N) $ の地震では、以下のことが起こります。 1. 電柱 $ i $ がまだ倒れていない場合、それが数直線における左または右の方向に、それぞれ $ \frac{1}{2} $ ずつの確率で倒れる。 2. 倒れようとしている電柱が、まだ倒れていない電柱に衝突した場合（電柱の最下部に衝突した場合を含む）、この電柱も同じ方向に倒れる。場合によってはこれが連鎖的に起こる。 ここで、1. で電柱がどちら方向に倒れるかは、他の電柱がどちら方向に倒れたかに関係しません。 以下の図は一回の地震での電柱の倒れ方の一例です。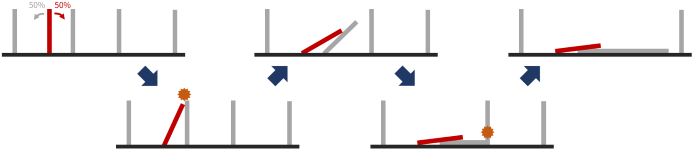  地震対策のため、$ t\ =\ 1,\ 2,\ \dots,\ N $ それぞれについて、ちょうど $ t $ 回目の地震ですべての電柱が倒れた状態になる確率を $ 2^N $ 倍した値を $ 998244353 $ で割った余りを求めてください。なお、出力すべき値は整数になることが証明できます。

入力は以下の形式で標準入力から与えられます。 > $ N $ $ H $ $ X_1 $ $ X_2 $ $ \cdots $ $ X_N $

$ t\ =\ 1,\ 2,\ \dots,\ N $ についての答えをその順番で空白区切りで出力してください。

### 制約 - $ 1\ \leq\ N\ \leq\ 2\ \times\ 10^5 $ - $ 1\ \leq\ H\ \leq\ 10^9 $ - $ 0\ \leq\ X_i\ \leq\ 10^9\ (1\ \leq\ i\ \leq\ N) $ - $ X_1,\ X_2,\ \dots,\ X_N $ はすべて異なる - 入力はすべて整数 ### Sample Explanation 1 以下の図は、この入力例における電柱の倒れ方の可能性を示しています。図中の分数はその状態になる確率を示しています。 !\[ \](https://img.atcoder.jp/arc177/1b1ec413ff3069cd13b19efd64b9c9d2.png) したがって、ちょうど $ 1,\ 2,\ 3 $ 回目の地震ですべての電柱が倒れた状態になる確率は、それぞれ $ \frac{1}{2},\ \frac{1}{4},\ \frac{1}{4} $ です。これを $ 8 $ 倍した $ 4,\ 2,\ 2 $ を出力しましょう。 ### Sample Explanation 2 以下の図は、この入力例における電柱の倒れ方の可能性を示しています。図中の分数はその状態になる確率を示しています。 !\[ \](https://img.atcoder.jp/arc177/f2ce4d20221071c814e204d8a2adc60d.png) したがって、ちょうど $ 1,\ 2,\ 3,\ 4 $ 回目の地震ですべての電柱が倒れた状態になる確率は、それぞれ $ 0,\ \frac{1}{4},\ \frac{1}{4},\ \frac{1}{2} $ です。これを $ 16 $ 倍した $ 0,\ 4,\ 4,\ 8 $ を出力しましょう。 ### Sample Explanation 3 ちょうど $ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8 $ 回目の地震ですべての電柱が倒れた状態になる確率は、それぞれ $ 0,\ \frac{1}{4},\ \frac{1}{8},\ \frac{3}{16},\ \frac{3}{32},\ \frac{7}{64},\ \frac{7}{64},\ \frac{1}{8} $ です。 ### Sample Explanation 4 $ 37 $ 回目の地震までにすべての電柱が倒れることはありません。ちょうど $ 38,\ 39,\ 40 $ 回目の地震ですべての電柱が倒れた状態になる確率は、それぞれ $ \frac{3}{8},\ \frac{3}{8},\ \frac{1}{4} $ です。