AT_arc190_b [ARC190B] L Partition

There is an $ N \times N $ grid. Let $ (i,j) $ denote the cell at the $ i $ -th row from the top and the $ j $ -th column from the left. For $ K = 1, 2, \ldots, N $ , a **level $ K $ L-shape** is a set of $ 2K - 1 $ cells that satisfies at least one of the following four conditions: - All cells reachable from a certain cell $ (i,j) $ by moving down or right between $ 0 $ and $ K-1 $ cells, inclusive (where $ 1 \leq i \leq N-K+1 $ , $ 1 \leq j \leq N-K+1 $ ). - All cells reachable from a certain cell $ (i,j) $ by moving down or left between $ 0 $ and $ K-1 $ cells, inclusive (where $ 1 \leq i \leq N-K+1 $ , $ K \leq j \leq N $ ). - All cells reachable from a certain cell $ (i,j) $ by moving up or right between $ 0 $ and $ K-1 $ cells, inclusive (where $ K \leq i \leq N $ , $ 1 \leq j \leq N-K+1 $ ). - All cells reachable from a certain cell $ (i,j) $ by moving up or left between $ 0 $ and $ K-1 $ cells, inclusive (where $ K \leq i \leq N $ , $ K \leq j \leq N $ ). You are given a cell $ (a,b) $ and $ Q $ queries $ k_1, \ldots, k_Q $ . For each $ i $ , print the number, modulo $ 998244353 $ , of ways to partition the entire grid into exactly one level $ 1 $ L-shape, one level $ 2 $ L-shape, $ \ldots $ , and one level $ N $ L-shape so that cell $ (a,b) $ is contained in the level $ k_i $ L-shape.

The input is given from Standard Input in the following format: > $ N $ $ a $ $ b $ $ Q $ $ k_1 $ $ \cdots $ $ k_Q $

Print $ Q $ lines. The $ i $ -th line should contain the number, modulo $ 998244353 $ , of ways to partition the grid into exactly one level $ 1 $ L-shape, one level $ 2 $ L-shape, $ \ldots $ , and one level $ N $ L-shape so that cell $ (a,b) $ is contained in the level $ k_i $ L-shape.

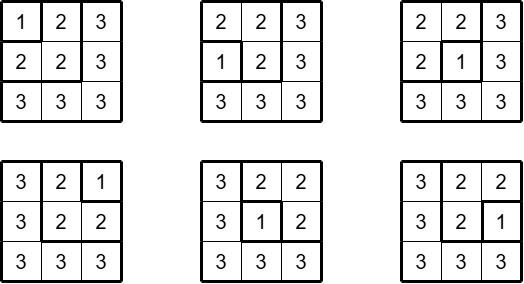
### Sample Explanation 1 The six ways shown in the following figure are the solutions. In the figure, an integer $ k $ in a cell means that the cell belongs to the level $ k $ L-shape.  ### Constraints - $ 1 \leq N \leq 10^7 $ - $ 1 \leq a \leq N $ - $ 1 \leq b \leq N $ - $ 1 \leq Q \leq \min\lbrace N, 200000 \rbrace $ - $ 1 \leq k_1 < \cdots < k_Q \leq N $ - All input values are integers.