AT_arc190_b [ARC190B] L Partition

$ N\times N $ のマス目があります．上から $ i $ 行目，左から $ j $ 列目のマスを $ (i,j) $ で表します． $ K=1,2,\ldots,N $ に対して，レベル $ K $ の **L 型**とは， $ 2K-1 $ 個からなるマスの集合であって次の $ 4 $ つのうち $ 1 $ つ以上に該当するものを指します． - あるマス $ (i,j) $ から下または右に $ 0 $ マス以上 $ K-1 $ マス以下進んだマス全体（ただし $ 1\leq i\leq N-K+1 $ , $ 1\leq j\leq N-K+1 $ ）． - あるマス $ (i,j) $ から下または左に $ 0 $ マス以上 $ K-1 $ マス以下進んだマス全体（ただし $ 1\leq i\leq N-K+1 $ , $ K\leq j\leq N $ ）． - あるマス $ (i,j) $ から上または右に $ 0 $ マス以上 $ K-1 $ マス以下進んだマス全体（ただし $ K\leq i\leq N $ , $ 1\leq j\leq N-K+1 $ ）． - あるマス $ (i,j) $ から上または左に $ 0 $ マス以上 $ K-1 $ マス以下進んだマス全体（ただし $ K\leq i\leq N $ , $ K\leq j\leq N $ ）． マス $ (a,b) $ および $ Q $ 個のクエリ $ k_1, \ldots, k_Q $ が与えられます． 各 $ i $ に対して，マス目全体をレベル $ 1, \ldots, N $ それぞれひとつずつの L 型に分割する方法であって，マス $ (a,b) $ がレベル $ k_i $ の L 型に含まれるようなものの個数を $ 998244353 $ で割った余りを答えてください．

入力は以下の形式で標準入力から与えられます． > $ N $ $ a $ $ b $ $ Q $ $ k_1 $ $ \cdots $ $ k_Q $

$ Q $ 行出力してください． $ i $ 行目にはマス目全体をレベル $ 1, \ldots, N $ それぞれひとつずつの L 型に分割する方法であって，マス $ (a,b) $ がレベル $ k_i $ の L 型に含まれるようなものの個数を $ 998244353 $ で割った余りを出力してください．

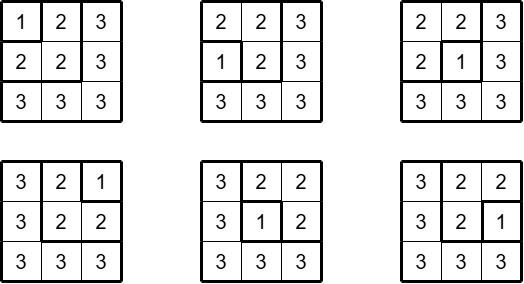
### Sample Explanation 1 以下の図で表される $ 6 $ 通りが解になります．図においてマスに整数 $ k $ が書かれていることは，そのマスがレベル $ k $ の L 型に含まれることを意味します．  ### Constraints - $ 1\leq N\leq 10^7 $ - $ 1\leq a\leq N $ - $ 1\leq b\leq N $ - $ 1\leq Q\leq \min\lbrace N, 200000\rbrace $ - $ 1\leq k_1 < \cdots < k_Q \leq N $ - 入力される値はすべて整数である