AT_arc196_b [ARC196B] Torus Loop
题目描述
有一个 $H$ 行 $W$ 列网格,每个格点放了一块瓷砖,瓷砖有如下两种:
- 类型 $A$:连接两个相邻边的中点的线段。

- 类型 $B$:连接两个相对边的中点的线段。
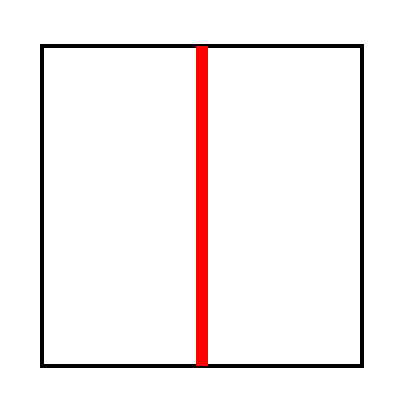
瓷砖可以旋转:$A$ 类瓷砖有四种旋转方式,$B$ 类瓷砖有两种旋转方式。
求出旋转瓷砖的方案数,使得将网格视为环面后,瓷砖上的线不存在“死胡同”。具体地,要求同时满足以下两个条件:
1. 以下两条同时满足或同时不满足:
- $(i,j)$ 有一端点为右边界中点。
- $(i,(j+1)\bmod W)$ 有一端点为左边界中点。
2. 以下两条同时满足或同时不满足:
- $(i,j)$ 有一端点为下边界中点。
- $((i+1)\bmod H,j)$ 有一端点为上边界中点。
符合条件的一种放置:
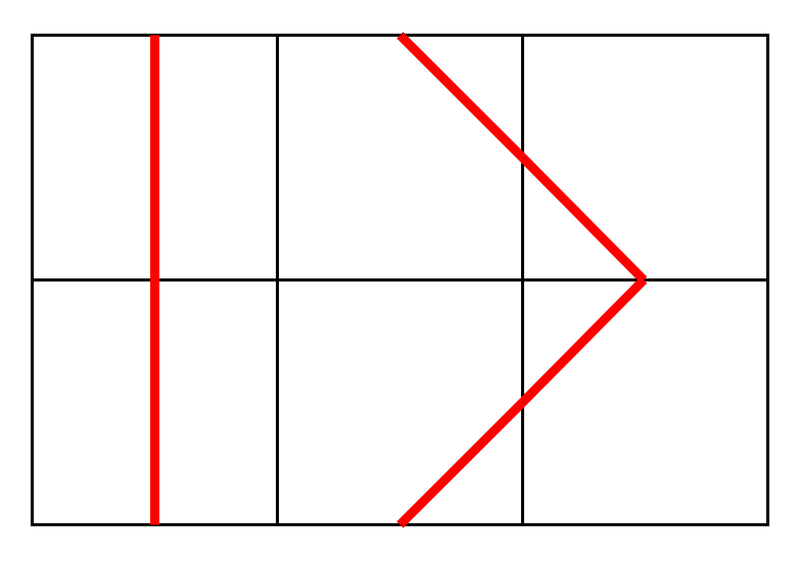
不符合条件的一种放置:
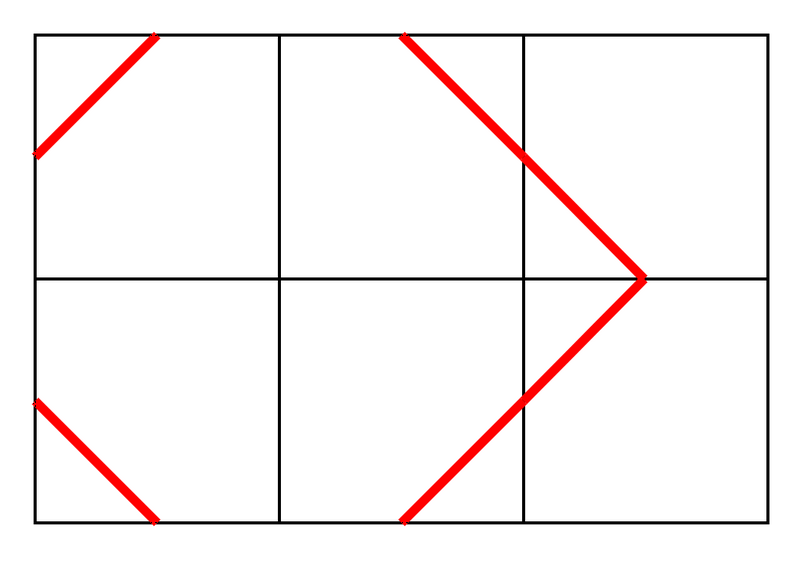
多组数据,对 $998244353$ 取模。
输入格式
多组数据,对于每组数据:
> $ H $ $ W $
>
> $ S_0 $
>
> $ S_1 $
>
> $ \vdots $
>
> $ S_{H-1} $
输出格式
每组数据输出一行,为方案数对 $998244353$ 取模后的值。
说明/提示
$ 1\ \le\ T\ \le\ 10^5 $;$ 2\ \le\ H,W \leq 10^6$;$ \sum HW\leq\ 10^6 $。