AT_arc197_a [ARC197A] Union of Grid Paths

你有一个 $H\times W$ 的网格，初始时网格中的格子都是白色的。 给你一个长度为 $H+W-2$、由 `D`、`R` 和 `?` 组成的字符串 $S$，你要执行若干次以下操作： - 走一条从 $(1,1)$ 到 $(H,W)$ 的路径，每一步只能选择向下或向右走一格，若 $S_i=$`D` 则第 $i$ 步只能选择往下走，若 $S_i=$`R` 则第 $i$ 步只能往右走。 - 把路径上经过的所有格子，包括开头结尾，全部染成黑色。 求你最多能够把多少个格子染成黑色。

多组数据。第一行一个整数 $T$ 表示数据组数。 对于每组数据：\ 第一行两个整数 $H,W$。\ 第二行一个长度为 $H+W-2$ 的、由 `D`、`R` 和 `?` 组成的字符串 $S$。

对于每组数据，一行一个整数表示答案。

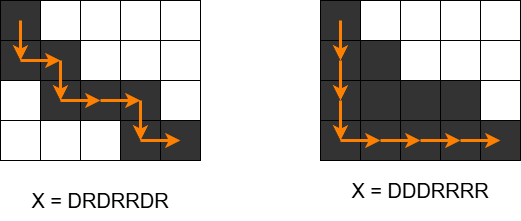
**数据范围** 保证 $1\le T\le 2\times 10^5,2\le H,W\le 2\times 10^5$，通过 $S$ 能够构造出的合法路径至少有一条。 保证单个测试点中 $\sum(H+W)\le 4\times 10^5$。 **样例解释** 对于第一组数据，用 $X$ 表示你所走的路径，如下两次操作可以把 $12$ 个格子染成黑色。  By @[chenxi2009](/user/1020063)