AT_arc197_a [ARC197A] Union of Grid Paths

There is an $ H\times W $ grid of cells. Let $ (h,w) $ denote the cell at the $ h $ -th row from the top and the $ w $ -th column from the left. Furthermore, you are given a string $ S = S_1\cdots S_{H+W-2} $ of length $ H+W-2 $ consisting of `D`, `R`, and `?`. Initially, all cells are painted white. You may perform the following operation, which consists of three steps, any number of times: 1. Choose a string $ X = X_1\cdots X_{H+W-2} $ of length $ H+W-2 $ satisfying all of the following. - $ X $ consists of exactly $ H-1 $ `D`s and $ W-1 $ `R`s. - For each $ 1 \le i \le H+W-2 $ , if $ S_i $ is `D` then $ X_i $ must also be `D`. - For each $ 1 \le i \le H+W-2 $ , if $ S_i $ is `R` then $ X_i $ must also be `R`. 2. Stand on cell $ (1,1) $ . Then for $ i=1,2,\ldots $ in order, move one cell in the direction indicated by $ X_i $ : if $ X_i $ is `D`, move down one cell; if $ X_i $ is `R`, move right one cell. It can be shown that if $ X $ satisfies the conditions in step 1, the destination cell always exists within the grid. 3. For every cell you visited in step 2 (including the starting and ending cells), if the cell is currently white, paint it black. Find the maximum possible number of cells that can be painted black in total. There are $ T $ test cases; solve each one.

The input is given from Standard Input in the following format: > $ T $ $ \text{case}_1 $ $ \vdots $ $ \text{case}_T $ Each case is given in the following format: > $ H $ $ W $ $ S $

Print $ T $ lines. The $ i $ -th line should contain the maximum number of cells that can be painted black for the $ i $ -th test case.

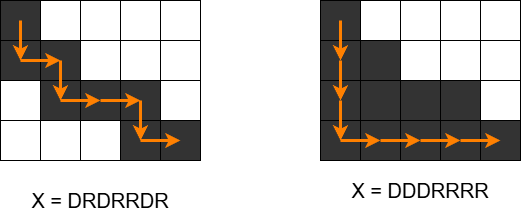
### Sample Explanation 1 For the first test case, by choosing $ X $ as `DRDRRDR` in the first operation and `DDDRRRR` in the second operation, you can paint $ 12 $ cells black.  ### Constraints - $ 1\le T\le 2\times 10^5 $ - $ 2\le H,W\le 2\times 10^5 $ - $ T,H,W $ are integers. - $ S $ is a string of length $ H+W-2 $ consisting of `D`, `R`, and `?`. - The number of `D`s in $ S $ is at most $ H-1 $ . - The number of `R`s in $ S $ is at most $ W-1 $ . - The sum of $ H+W $ over all test cases is at most $ 4\times 10^5 $ .