AT_arc197_a [ARC197A] Union of Grid Paths
Description
$ H\times W $ のマス目があります.上から $ h $ 行目,左から $ w $ 列目のマスを $ (h,w) $ で表します.さらに,`D`, `R`, `?` からなる長さ $ H+W-2 $ の文字列 $ S=S_1\cdots S_{H+W-2} $ が与えられます.
はじめ,すべてのマスは白色で塗られています.あなたは次の $ 3 $ つの手順からなる操作を何度でも行うことができます:
1. 以下の条件をすべて満たす長さ $ H+W-2 $ の文字列 $ X=X_1\cdots X_{H+W-2} $ をひとつ選ぶ.
- $ X $ は $ H-1 $ 個の `D` および $ W-1 $ 個の `R` からなる.
- $ 1\leq i\leq H+W-2 $ に対して, $ S_i $ が `D` ならば $ X_i $ も `D` である.
- $ 1\leq i\leq H+W-2 $ に対して, $ S_i $ が `R` ならば $ X_i $ も `R` である.
2. マス $ (1,1) $ に立つ.さらに $ i=1,2,\ldots $ の順に,文字 $ X_i $ の表す方向に $ 1 $ マス移動する.つまり, $ X_i $ が `D` ならば下方向, $ X_i $ が `R` ならば右方向に $ 1 $ マス移動する.なお, $ X $ が手順 1 の条件を満たすとき,移動先のマスは必ずマス目内に存在することが証明できる.
3. 手順 2 においてあなたが通ったすべてのマス(最初・最後のマスも含む)について,そのマスが白色で塗られているならば,黒色で塗る.
最終的に黒色で塗ることができるマスの個数としてありうる最大値を求めてください.
$ T $ 個のテストケースが与えられるので,それぞれについて解いてください.
Input Format
入力は以下の形式で標準入力から与えられます.
> $ T $ $ \text{case}_1 $ $ \vdots $ $ \text{case}_T $
各ケースは以下の形式で与えられます.
> $ H $ $ W $ $ S $
Output Format
$ T $ 行出力してください. $ i $ 行目には $ i $ 番目のテストケースについて,最終的に黒色で塗ることができるマスの個数としてありうる最大値を出力してください.
Explanation/Hint
### Sample Explanation 1
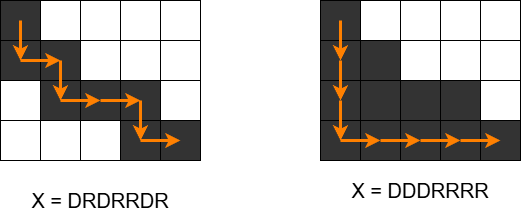
$ 1 $ つめのテストケースについて, $ 1 $ 回目に $ X $ として `DRDRRDR` を選び, $ 2 $ 回目に $ X $ として `DDDRRRR` を選ぶことで, $ 12 $ 個のマスを黒く塗ることができます.
### Constraints
- $ 1\leq T\leq 2\times 10^5 $
- $ 2\leq H, W\leq 2\times 10^5 $
- $ T,H,W $ は整数.
- $ S $ は `D`, `R`, `?` からなる長さ $ H+W-2 $ の文字列.
- $ S $ に含まれる `D` の個数は $ H-1 $ 以下.
- $ S $ に含まれる `R` の個数は $ W-1 $ 以下.
- すべてのテストケースにわたる $ H+W $ の総和は $ 4\times 10^5 $ 以下.