AT_arc197_d [ARC197D] Ancestor Relation

给你一个 $N\times N$ 的矩阵 $A$，其中每一项只会是 $0$ 或 $1$。 请找出有多少种不同的 $N$ 个点的树 $G$，使得： $\forall 1\le i,j\le N,A_{i,j}=1$，当且仅当 $i=j$，或以结点 $1$ 为根时，$i$ 是 $j$ 的祖先或 $j$ 是 $i$ 的祖先。 两棵树不同，当且仅当存在两个结点 $i,j$，在其中一棵树上它们之间有直接连边而在另一棵树上没有。 请输出答案对 $998244353$ 取模后的结果。

多组数据。第一行一个整数 $T$，表示接下来有 $T$ 组数据。 对于每组数据：\ 第一行一个整数 $N$。\ 接下来 $N$ 行，每行 $N$ 个整数，构成一个由 $0$ 和 $1$ 组成的大小为 $N\times N$ 的矩阵 $A$。

每组数据输出一行一个整数，表示答案对 $998244353$ 取模的结果。

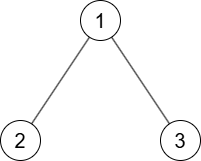
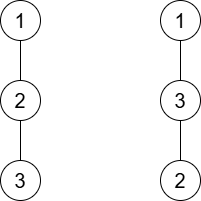
**数据范围** 保证 $1\le T\le 10^5,2\le N\le 400,A_{i,j}\in\{0,1\},A_{i,i}=1,A_{i,j}=A_{j,i}$。 保证一个测试点中 $\sum N^2\le 400^2=1.6\times 10^5$。 **样例解释** 对于第一组数据，唯一满足条件的树 $G$ 如下所示：  对于第二组数据，唯二满足条件的树 $G$ 如下所示：  By @[chenxi2009](/user/1020063)