AT_arc197_d [ARC197D] Ancestor Relation

You are given an $ N\times N $ matrix $ A = (A_{i,j}) $ ( $ 1\le i,j\le N $ ) whose entries are $ 0 $ or $ 1 $ . Find, modulo $ 998244353 $ , the number of trees $ G $ on $ N $ vertices numbered $ 1 $ to $ N $ that satisfy the following condition. - $ A_{i,j}=1 $ if and only if at least one of the following holds: - When $ G $ is rooted at vertex $ 1 $ , Vertex $ j $ is an ancestor of vertex $ i $ . That is, vertex $ j $ lies on the unique path in $ G $ between vertices $ 1 $ and $ i $ . - When $ G $ is rooted at vertex $ 1 $ , Vertex $ i $ is an ancestor of vertex $ j $ . That is, vertex $ i $ lies on the unique path in $ G $ between vertices $ 1 $ and $ j $ . Here, the endpoints of a path are considered to be on that path. Note that $ G $ being a tree guarantees uniqueness of the path between any two vertices. There are $ T $ test cases; solve each one.

The input is given from Standard Input in the following format: > $ T $ $ \text{case}_1 $ $ \vdots $ $ \text{case}_T $ Each case is given in the following format: > $ N $ $ A_{1,1} $ $ \cdots $ $ A_{1,N} $ $ \vdots $ $ A_{N,1} $ $ \cdots $ $ A_{N,N} $

Print $ T $ lines. The $ i $ -th line should contain the number, modulo $ 998244353 $ , of trees $ G $ satisfying the conditions for the $ i $ -th test case.

### Sample Explanation 1 In the first test case, the following one tree $ G $ satisfies the condition: 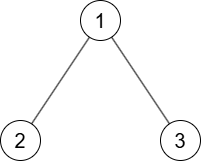 In the second test case, the following two trees $ G $ satisfy the condition: 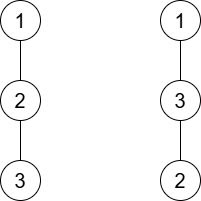 ### Constraints - $ 1\leq T\leq 10^5 $ - $ 2\leq N\leq 400 $ - $ A_{i,j}\in \lbrace 0,1\rbrace $ $ (1\leq i,j\leq N) $ - $ A_{i,i}=1 $ $ (1\leq i\leq N) $ - $ A_{i,j}=A_{j,i} $ $ (1\leq i,j\leq N) $ - The sum of $ N^2 $ over all test cases is at most $ 400^2 $ .