AT_arc197_d [ARC197D] Ancestor Relation

$ N\times N $ 行列 $ A = (A_{i,j}) $ ( $ 1\leq i,j\leq N $ ) が与えられます． $ A $ の成分は $ 0 $ または $ 1 $ です． 頂点に $ 1 $ から $ N $ までの番号が付けられた $ N $ 頂点の木 $ G $ であって，次の条件を満たすものの個数を $ 998244353 $ で割った余りを求めてください． - $ A_{i,j}=1 $ であることと，以下の $ 2 $ 条件のうち少なくともひとつが成り立つことは同値である： - 頂点 $ 1 $ を根としたとき頂点 $ j $ は頂点 $ i $ の祖先である．つまり頂点 $ j $ は，頂点 $ 1, i $ を結ぶ $ G $ 上のパス上にある． - 頂点 $ 1 $ を根としたとき頂点 $ i $ は頂点 $ j $ の祖先である．つまり頂点 $ i $ は，頂点 $ 1, j $ を結ぶ $ G $ 上のパス上にある． ただし，パスの端点もパス上にあると見なします． $ G $ は木であるとき， $ 2 $ 頂点を結ぶ $ G $ 上のパスは一意に存在することにも注意してください． $ T $ 個のテストケースが与えられるので，それぞれについて解いてください．

入力は以下の形式で標準入力から与えられます． > $ T $ $ \text{case}_1 $ $ \vdots $ $ \text{case}_T $ 各ケースは以下の形式で与えられます． > $ N $ $ A_{1,1} $ $ \cdots $ $ A_{1,N} $ $ \vdots $ $ A_{N,1} $ $ \cdots $ $ A_{N,N} $

$ T $ 行出力してください． $ i $ 行目には $ i $ 番目のテストケースについて，条件を満たす $ N $ 頂点の木 $ G $ の個数を $ 998244353 $ で割った余りを出力してください．

### Sample Explanation 1 $ 1 $ 番目のテストケースでは次の $ 1 $ つの $ G $ が条件を満たします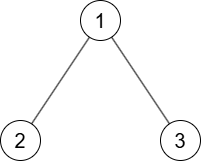．  $ 2 $ 番目のテストケースでは次の $ 2 $ つの $ G $ が条件を満たします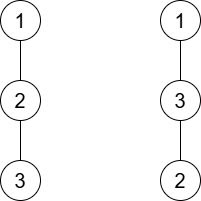．  ### Constraints - $ 1\leq T\leq 10^5 $ - $ 2\leq N\leq 400 $ - $ A_{i,j}\in \lbrace 0,1\rbrace $ $ (1\leq i,j\leq N) $ - $ A_{i,i}=1 $ $ (1\leq i\leq N) $ - $ A_{i,j}=A_{j,i} $ $ (1\leq i,j\leq N) $ - すべてのテストケースにわたる $ N^2 $ の総和は $ 400^2 $ 以下．