AT_arc197_e [ARC197E] Four Square Tiles

You are given positive integers $ N $ , $ H $ , and $ W $ , with $ H,W \le 3N-1 $ . Find the number, modulo $ 998244353 $ , of ways to place four $ N\times N $ square tiles on an $ H\times W $ grid that satisfy all of the following conditions. - Each tile exactly covers $ N^2 $ cells of the grid. - No cell is covered by more than one tile. Here, the tiles are indistinguishable. There are $ T $ test cases; solve each one.

The input is given from Standard Input in the following format: > $ T $ $ \text{case}_1 $ $ \vdots $ $ \text{case}_T $ Each case is given in the following format: > $ N $ $ H $ $ W $

Print $ T $ lines. The $ i $ -th line should contain the number, modulo $ 998244353 $ , of valid ways to place the tiles for the $ i $ -th test case.

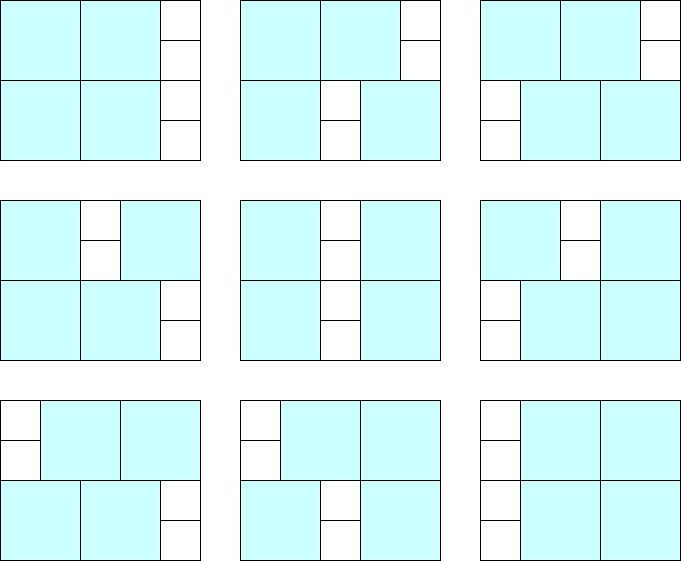
### Sample Explanation 1 For the first test case, there are $ 9 $ ways as illustrated in the following figure:  ### Constraints - $ 1\le T\le 2\times 10^5 $ - $ 1\le N,H,W\le 10^9 $ - $ H,W\le 3N-1 $ - All input values are integers.