AT_arc197_e [ARC197E] Four Square Tiles

正整数 $ N, H, W $ が与えられます．ただし， $ H, W \leq 3N-1 $ が成り立ちます． $ H\times W $ のマス目に $ N\times N $ の正方形のタイルを $ 4 $ 個置く方法であって，以下の条件をすべて満たすものの個数を $ 998244353 $ で割った余りを求めてください． - 各タイルは，マス目の ちょうど $ N^2 $ 個のマスを完全に覆う． - ひとつのマスが複数のタイルによって覆われてはならない． ただし，タイル同士は区別しません． $ T $ 個のテストケースが与えられるので，それぞれについて解いてください．

入力は以下の形式で標準入力から与えられます． > $ T $ $ \text{case}_1 $ $ \vdots $ $ \text{case}_T $ 各ケースは以下の形式で与えられます． > $ N $ $ H $ $ W $

$ T $ 行出力してください． $ i $ 行目には $ i $ 番目のテストケースについて，条件を満たすようにタイルを置く方法の個数を $ 998244353 $ で割った余りを出力してください．

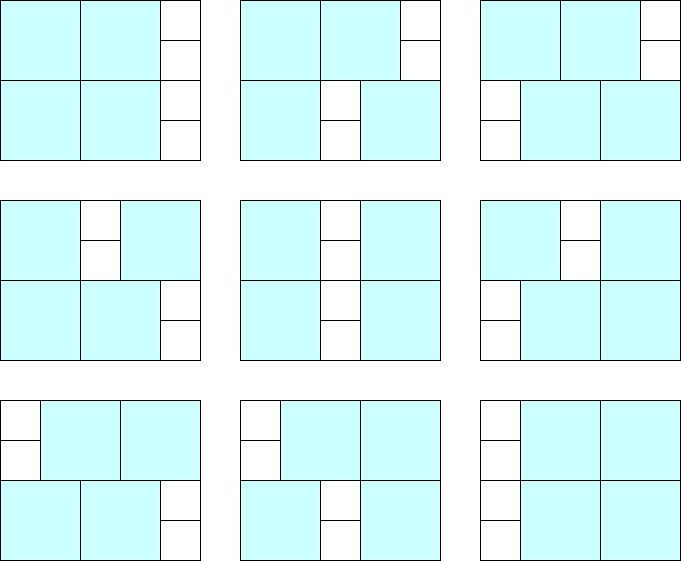
### Sample Explanation 1 $ 1 $ つめのテストケースについて，次の図で示す $ 9 $ 通りの方法があります．  ### Constraints - $ 1\leq T\leq 2\times 10^5 $ - $ 1\leq N,H,W\leq 10^9 $ - $ H,W\leq 3N - 1 $ - 入力される値はすべて整数