AT_arc197_e [ARC197E] Four Square Tiles

给你三个整数 $N,H,W$，保证 $H,W\le 3N-1$。 求把四个 $N\times N$ 的方形瓷砖铺在 $H\times W$ 的网格上的方案数，瓷砖不能相互覆盖，不能斜着摆放，每个瓷砖必须完整地覆盖 $N^2$ 个格子。 方形瓷砖之间是完全相同的，也就是说两个摆放方案不同当且仅当存在一个方格在一种方案里被瓷砖覆盖，在另一种方案里没有。 输出答案对 $998244353$ 取模的结果。

多组数据。第一行一个整数 $T(1\le T\le 2\times 10^5)$，表示数据组数。 对于每组数据，一行三个整数 $N,H,W(1\le N,H,W\le 10^9)$。

对于每组数据，输出一行一个整数表示答案对 $998244353$ 取模后的结果。

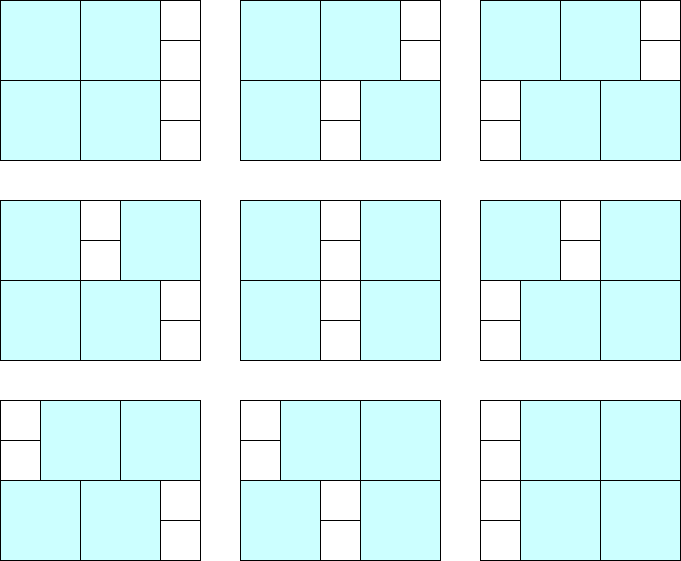
**样例解释** 对于第一组数据，$9$ 种摆放方式如下：  By @[chenxi2009](/user/1020063)