AT_arc199_c [ARC199C] Circular Tree Embedding
题目描述
在本题中,将编号为 $1,2,\ldots,N$ 的顶点组成的、边没有编号的 $N$ 个顶点的树,称为 $N$ 个顶点的树。
当 $N$ 个顶点的树 $T$ 和 $1,2,\ldots,N$ 的一个排列 $Q=(Q_1,Q_2,\ldots,Q_N)$ 满足以下条件时,称排列 $Q$ 是树 $T$ 的**良好排列**。
> 在圆周上等间隔地按逆时针顺序排列 $N$ 个点 $1,2,\ldots,N$。对于树 $T$ 的每一条边 $\lbrace u,v\rbrace$,在圆上连接 $Q_u$ 和 $Q_v$ 两个点,画一条线段。此时,画出的 $N-1$ 条线段中,任意选取两条线段,除了端点外都不会有交点。
给定 $M$ 个 $1,2,\ldots,N$ 的排列 $P^1=(P^1_1,P^1_2,\ldots,P^1_N),P^2=(P^2_1,P^2_2,\ldots,P^2_N),\ldots,P^M=(P^M_1,P^M_2,\ldots,P^M_N)$。
请计算有多少个 $N$ 个顶点的树,使得 $P^1,P^2,\ldots,P^M$ 全部都是这些树的良好排列。答案对 $998244353$ 取模。
输入格式
输入通过标准输入给出,格式如下:
> $N$ $M$ $P^1_1$ $P^1_2$ $\ldots$ $P^1_N$ $P^2_1$ $P^2_2$ $\ldots$ $P^2_N$
> $\vdots$
> $P^M_1$ $P^M_2$ $\ldots$ $P^M_N$
输出格式
输出满足 $P^1,P^2,\ldots,P^M$ 全部为良好排列的 $N$ 个顶点的树的个数,对 $998244353$ 取模。
说明/提示
### 限制条件
- $2\leq N,M\leq 500$
- $P^1,P^2,\ldots,P^M$ 均为 $1,2,\ldots,N$ 的排列
- 所有输入均为整数
### 样例解释 1
例如,对于下图中的两棵树,$P^1,P^2$ 都是良好排列。(蓝色数字表示顶点编号。)

另一方面,对于下图中的树,$P^2$ 不是良好排列。
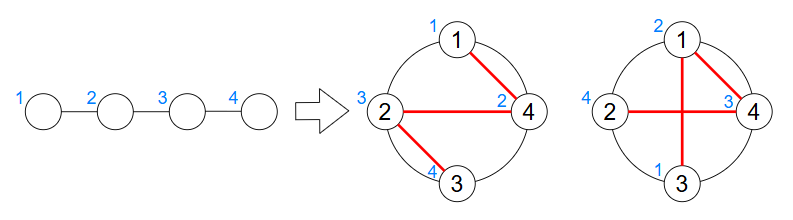
使得 $P^1,P^2$ 均为良好排列的 $4$ 个顶点的树共有 $8$ 棵。
由 ChatGPT 4.1 翻译