AT_arc199_c [ARC199C] Circular Tree Embedding

In this problem, we simply call a tree with $ N $ vertices numbered $ 1,2,\ldots,N $ and unnumbered edges an $ N $ -vertex tree. When an $ N $ -vertex tree $ T $ and a permutation $ Q=(Q_1,Q_2,\ldots,Q_N) $ of $ (1,2,\ldots,N) $ satisfy the following condition, the permutation $ Q $ is called a **good permutation** of tree $ T $ : > There are $ N $ points $ 1,2,\ldots,N $ arranged counterclockwise at equal intervals on a circle in this order. For each edge $ \lbrace u,v\rbrace $ of tree $ T $ , draw a line segment connecting the two points $ Q_u,Q_v $ . Then, among the $ N-1 $ line segments drawn, no two of them have a common point except at their endpoints. You are given $ M $ permutations of $ (1,2,\ldots,N) $ : $ P^1=(P^1_1,P^1_2,\ldots,P^1_N),P^2=(P^2_1,P^2_2,\ldots,P^2_N),\ldots,P^M=(P^M_1,P^M_2,\ldots,P^M_N) $ . Find the number, modulo $ 998244353 $ , of $ N $ -vertex trees such that $ P^1,P^2,\ldots,P^M $ are all good permutations.

The input is given from Standard Input in the following format: > $ N $ $ M $ $ P^1_1 $ $ P^1_2 $ $ \ldots $ $ P^1_N $ $ P^2_1 $ $ P^2_2 $ $ \ldots $ $ P^2_N $ $ \vdots $ $ P^M_1 $ $ P^M_2 $ $ \ldots $ $ P^M_N $

Output the number, modulo $ 998244353 $ , of $ N $ -vertex trees such that $ P^1,P^2,\ldots,P^M $ are all good permutations.

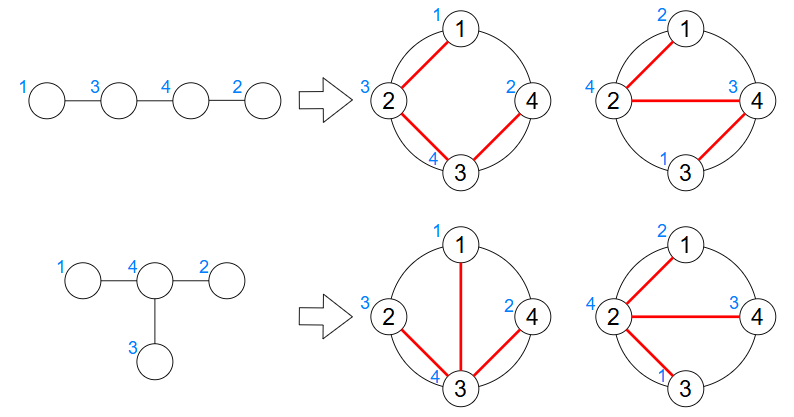
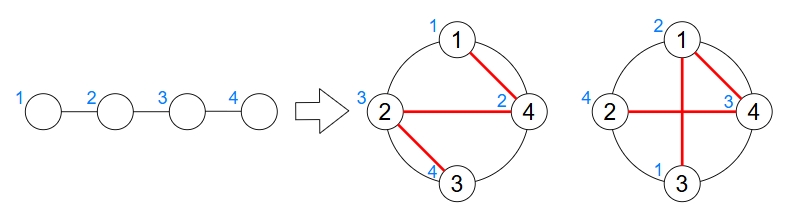
### Sample Explanation 1 For example, for the following two trees, both $ P^1,P^2 $ are good permutations. (The blue numbers represent vertex numbers.)  On the other hand, for the following tree, $ P^2 $ is not a good permutation.  There are $ 8 $ four-vertex trees in total such that both $ P^1,P^2 $ are good permutations. ### Constraints - $ 2\leq N,M\leq 500 $ - $ P^1,P^2,\ldots,P^M $ are permutations of $ (1,2,\ldots,N) $ . - All input values are integers.