AT_arc199_c [ARC199C] Circular Tree Embedding

この問題では，頂点に $ 1,2,\ldots,N $ の番号が付けられ，辺に番号が付いていない $ N $ 頂点の木を単に $ N $ 頂点の木と呼ぶことにします． $ N $ 頂点の木 $ T $ および $ (1,2,\ldots,N) $ の順列 $ Q=(Q_1,Q_2,\ldots,Q_N) $ が次の条件を満たすとき，順列 $ Q $ は木 $ T $ の **良い順列** であると呼びます． > 円周上に $ N $ 個の点 $ 1,2,\ldots,N $ がこの順で反時計回りに等間隔で配置されている．木 $ T $ の各辺 $ \lbrace u,v\rbrace $ に対して $ 2 $ 点 $ Q_u,Q_v $ を結ぶ線分を書き込む．このとき，書き込まれた $ N-1 $ 本の線分のうちどの $ 2 $ 本を選んでも，それらは端点を除いて共有点を持たない． $ M $ 個の $ (1,2,\ldots,N) $ の順列 $ P^1=(P^1_1,P^1_2,\ldots,P^1_N),P^2=(P^2_1,P^2_2,\ldots,P^2_N),\ldots,P^M=(P^M_1,P^M_2,\ldots,P^M_N) $ が与えられます． $ P^1,P^2,\ldots,P^M $ が全て良い順列となるような $ N $ 頂点の木の個数を $ 998244353 $ で割った余りを求めて下さい．

入力は以下の形式で標準入力から与えられる． > $ N $ $ M $ $ P^1_1 $ $ P^1_2 $ $ \ldots $ $ P^1_N $ $ P^2_1 $ $ P^2_2 $ $ \ldots $ $ P^2_N $ $ \vdots $ $ P^M_1 $ $ P^M_2 $ $ \ldots $ $ P^M_N $

$ P^1,P^2,\ldots,P^M $ が全て良い順列となるような $ N $ 頂点の木の個数を $ 998244353 $ で割った余りを出力せよ．

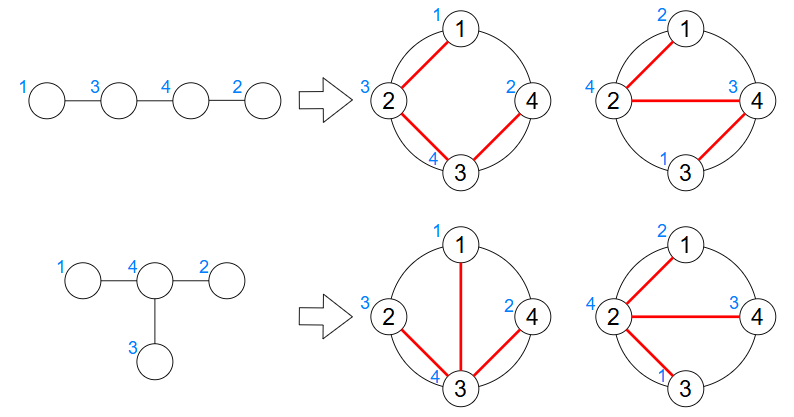
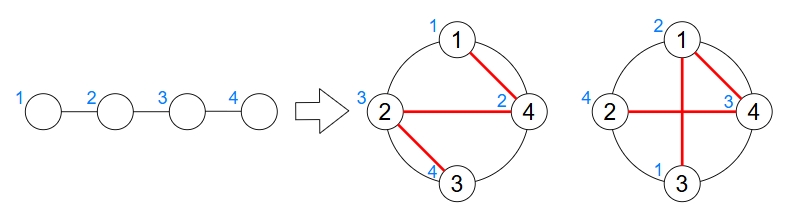
### Sample Explanation 1 たとえば以下の $ 2 $ つの木に対して， $ P^1,P^2 $ はどちらも良い順列です．（青い数字は頂点番号を表しています．）  一方，以下の木に対して $ P^2 $ は良い順列ではありません．  $ P^1,P^2 $ がともに良い順列となるような $ 4 $ 頂点の木は全部で $ 8 $ つあります． ### Constraints - $ 2\leq N,M\leq 500 $ - $ P^1,P^2,\ldots,P^M $ は $ (1,2,\ldots,N) $ の順列 - 入力は全て整数