AT_arc201_e [ARC201E] Total Area of Bounding Boxes

There are $ N $ points numbered $ 1,2, \dots, N $ on the $ 2 $ -dimensional plane. The coordinates of point $ i $ are $ (i,Y_i) $ . In this problem, it is guaranteed that $ Y=(Y_1,Y_2,\dots ,Y_N) $ is a permutation of $ (1,2, \dots ,N) $ . Find the sum of the areas of bounding boxes for all subsets $ S $ of $ \lbrace \texttt{point}\,1,\texttt{point}\,2,\dots ,\texttt{point}\,N \rbrace $ with at least $ 2 $ elements, modulo $ 998244353 $ . The bounding box for $ S $ refers to the minimum area rectangle with sides parallel to the $ x $ -axis that contains all points in $ S $ inside or on the boundary.

The input is given from Standard Input in the following format: > $ N $ $ Y_1 $ $ Y_2 $ $ \ldots $ $ Y_N $

Output the sum, modulo $ 998244353 $ , of the areas of bounding boxes.

### Sample Explanation 1 Each subset and the area of its bounding box are shown in the figure below. Output the sum of areas, which is $ 50 $ . 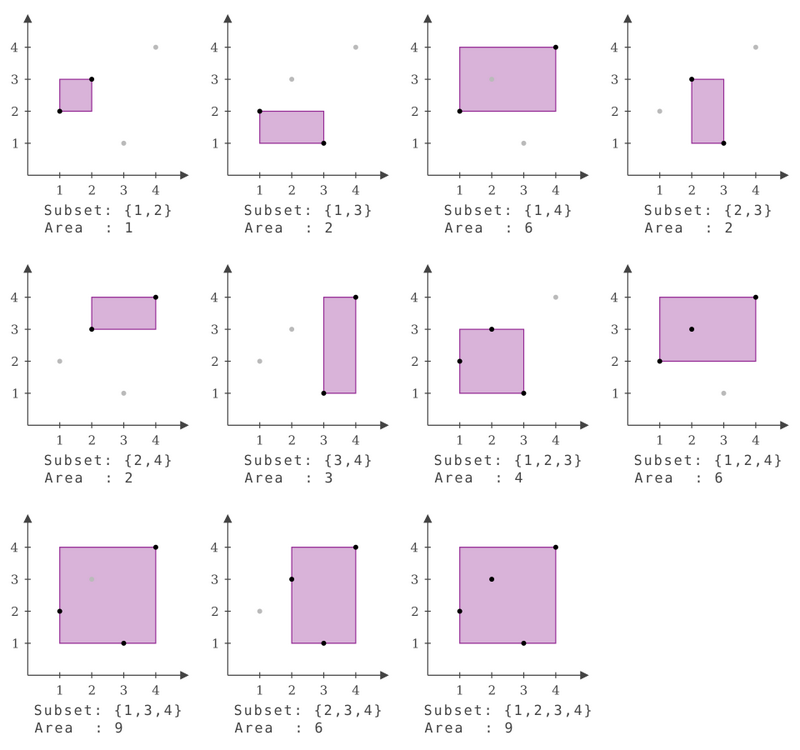 ### Constraints - $ 2 \le N \le 2 \times 10^5 $ - $ Y $ is a permutation of $ (1,2, \dots ,N) $ . - All input values are integers.