AT_arc201_e [ARC201E] Total Area of Bounding Boxes

$ 2 $ 次元平面上に $ 1,2, \dots, N $ の番号がついた $ N $ 個の点があります。 点 $ i $ の座標は $ (i,Y_i) $ です。 なお、この問題では $ Y=(Y_1,Y_2,\dots ,Y_N) $ は $ (1,2, \dots ,N) $ の順列であることが保証されます。 $ \lbrace \texttt{点} 1,\texttt{点} 2,\dots ,\texttt{点} N \rbrace $ の要素数 $ 2 $ 以上の部分集合 $ S $ 全てに対するバウンディングボックスの面積の総和を $ 998244353 $ で割った余りを求めて下さい。 $ S $ に対するバウンディングボックスとは、 $ S $ に含まれる全ての点を内部または周上に含んでかつ $ x $ 軸に平行な辺を持つような長方形のうち、面積が最小であるものを指します。

入力は以下の形式で標準入力から与えられる。 > $ N $ $ Y_1 $ $ Y_2 $ $ \ldots $ $ Y_N $

バウンディングボックスの面積の総和を $ 998244353 $ で割った余りを出力せよ。

### Sample Explanation 1 各部分集合とバウンディングボックスの面積は下図の通りです。面積の総和である $ 50 $ を出力します。 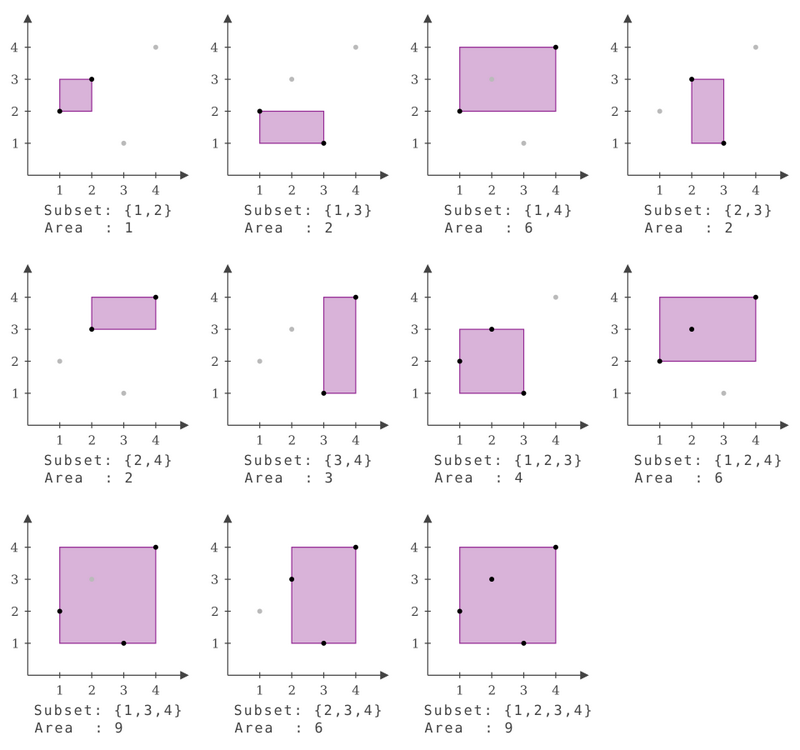 ### Constraints - $ 2 \le N \le 2 \times 10^5 $ - $ Y $ は $ (1,2, \dots ,N) $ の順列 - 入力される値は全て整数