AT_arc201_e [ARC201E] Total Area of Bounding Boxes
题目描述
在二维平面上有 $N$ 个编号为 $1,2,\dots,N$ 的点。第 $i$ 个点的坐标为 $(i, Y_i)$。此外,本题保证 $Y=(Y_1, Y_2, \dots, Y_N)$ 是 $(1,2,\dots,N)$ 的一个排列。
请计算所有元素个数不少于 $2$ 的 $\{\texttt{点}\ 1, \texttt{点}\ 2, \dots, \texttt{点}\ N\}$ 的子集 $S$ 的最小包围盒(bounding box)面积之和,并对 $998244353$ 取模。
对于子集 $S$,其最小包围盒指的是包含 $S$ 内所有点,且边平行于 $x$ 轴的最小面积矩形。
输入格式
输入通过标准输入按以下格式给出。
> $N$ $Y_1$ $Y_2$ $\ldots$ $Y_N$
输出格式
输出所有子集的最小包围盒面积之和对 $998244353$ 取模的结果。
说明/提示
## 限制条件
- $2 \leq N \leq 2 \times 10^5$
- $Y$ 是 $(1,2,\dots,N)$ 的一个排列
- 输入的所有值均为整数
## 样例解释 1
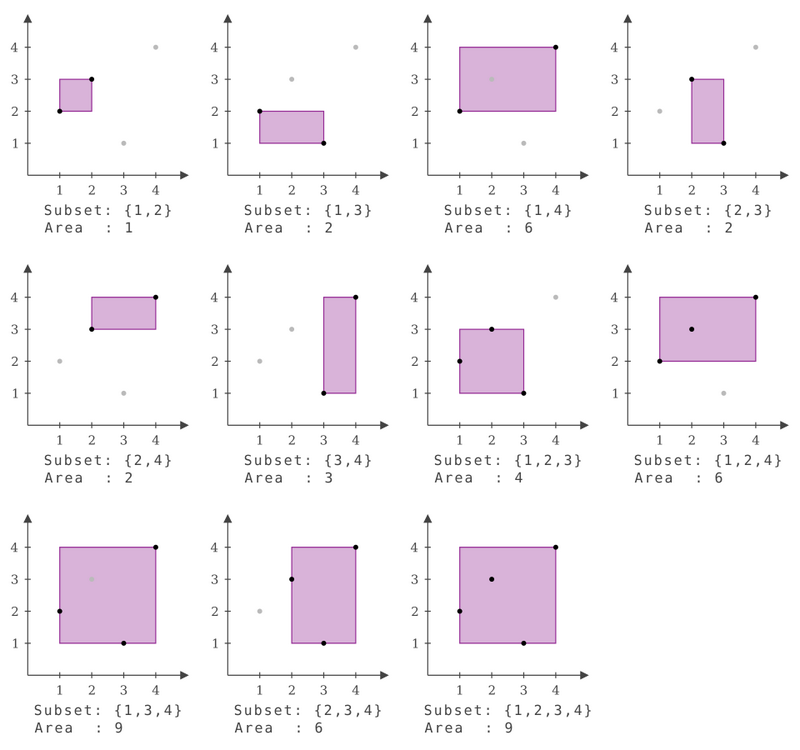
每个子集及其最小包围盒的面积如下图所示。面积总和为 $50$,输出 $50$。
由 ChatGPT 4.1 翻译