AT_arc205_d [ARC205D] Non-Ancestor Matching

You are given a rooted tree with $ N $ vertices numbered from $ 1 $ to $ N $ . Vertex $ 1 $ is the root, and the parent of vertex $ i $ $ (2 \le i \le N) $ is vertex $ p_i $ $ (1\le p_i < i) $ . Initially, all vertices are colored white. You can perform the following sequence of operations zero or more times. - Choose a pair of integers $ (u,v) $ that satisfies all of the following conditions. - $ 1\le u < v \le N $ - Both vertices $ u $ and $ v $ are colored white. - $ u $ is **not** an ancestor of $ v $ . - Color vertices $ u $ and $ v $ black. Here, " $ u $ is not an ancestor of $ v $ " means that you cannot reach vertex $ u $ from vertex $ v $ no matter how many times you perform the operation of moving to the parent of the current vertex. Find the maximum number of operations you can perform when you perform operations in an appropriate order. You are given $ T $ test cases, so find the answer for each of them.

The input is given from Standard Input in the following format: > $ T $ $ \text{case}_1 $ $ \text{case}_2 $ $ \vdots $ $ \text{case}_T $ Each test case $ \text{case}_i $ is given in the following format: > $ N $ $ p_2 $ $ p_3 $ $ \ldots $ $ p_N $

Output $ T $ lines. The $ i $ -th line $ (1\le i\le T) $ should contain the answer for the $ i $ -th test case.

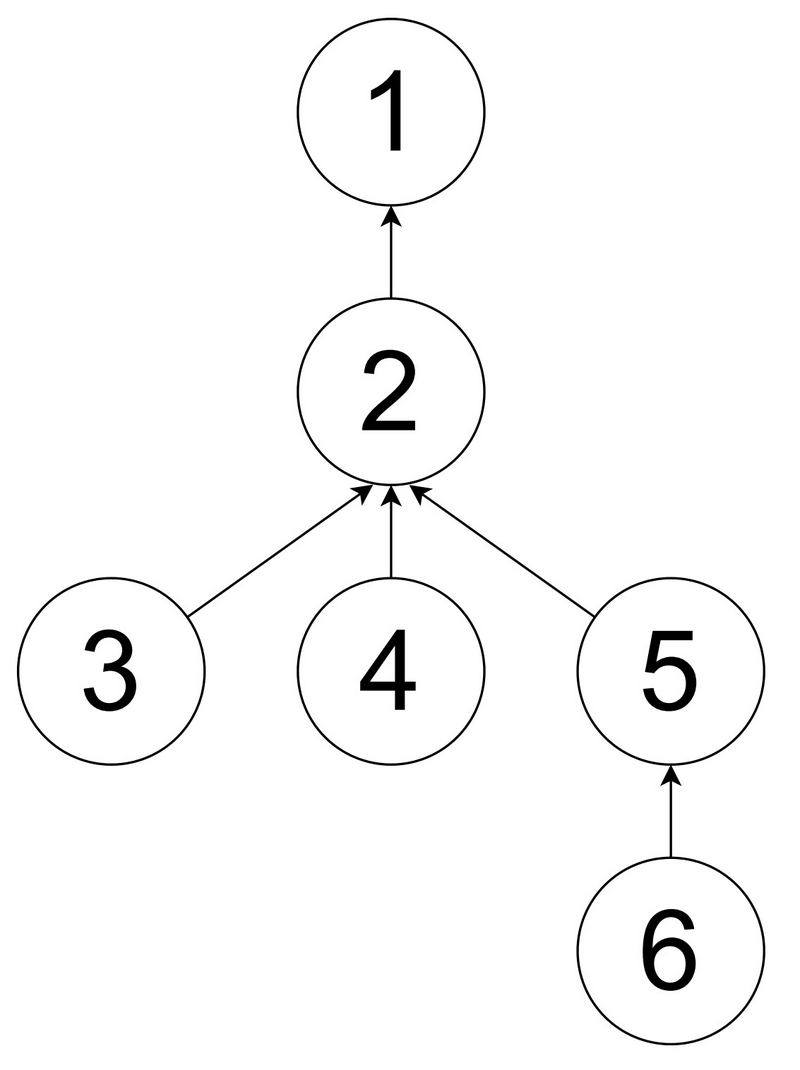
### Sample Explanation 1 Consider the first test case.  You can perform two operations as follows. - Choose $ (u,v)=(3,5) $ . Color vertices $ 3 $ and $ 5 $ black. - Choose $ (u,v)=(4,6) $ . Color vertices $ 4 $ and $ 6 $ black. You cannot perform more than two operations, so output $ 2 $ on the first line. ### Constraints - $ 1\le T\le 5\times 10^4 $ - $ 2\le N\le 5\times 10^5 $ - $ 1\le p_i < i $ - The sum of $ N $ over all test cases is at most $ 5\times 10^5 $ . - All input values are integers.