AT_arc205_d [ARC205D] Non-Ancestor Matching

頂点に $ 1 $ から $ N $ までの番号がついた $ N $ 頂点の根付き木が与えられます。頂点 $ 1 $ が根で、頂点 $ i $ $ (2 \le i \le N) $ の親は頂点 $ p_i $ $ (1\le p_i < i) $ です。はじめ、全ての頂点は白で塗られています。 あなたは以下の一連の操作を $ 0 $ 回以上何回でも行うことができます。 - 以下の条件を全て満たす整数の組 $ (u,v) $ を選ぶ。 - $ 1\le u < v \le N $ - 頂点 $ u $ と頂点 $ v $ はどちらも白で塗られている。 - $ u $ は $ v $ の祖先 **ではない**。 - 頂点 $ u $ と頂点 $ v $ を黒で塗る。 ただし、「 $ u $ は $ v $ の祖先ではない」とは頂点 $ v $ から今いる頂点の親に移動する操作を何回行っても頂点 $ u $ に到達できないことを意味します。 あなたが適切な順序で操作を行ったとき、最大で何回操作ができるか求めてください。 $ T $ 個のテストケースが与えられるので、それぞれについて答えを求めてください。

入力は以下の形式で標準入力から与えられる。 > $ T $ $ \text{case}_1 $ $ \text{case}_2 $ $ \vdots $ $ \text{case}_T $ 各テストケース $ \text{case}_i $ は以下の形式で与えられる。 > $ N $ $ p_2 $ $ p_3 $ $ \ldots $ $ p_N $

$ T $ 行出力せよ。 $ i $ 行目 $ (1\le i\le T) $ には $ i $ 番目のテストケースについての答えを出力せよ。

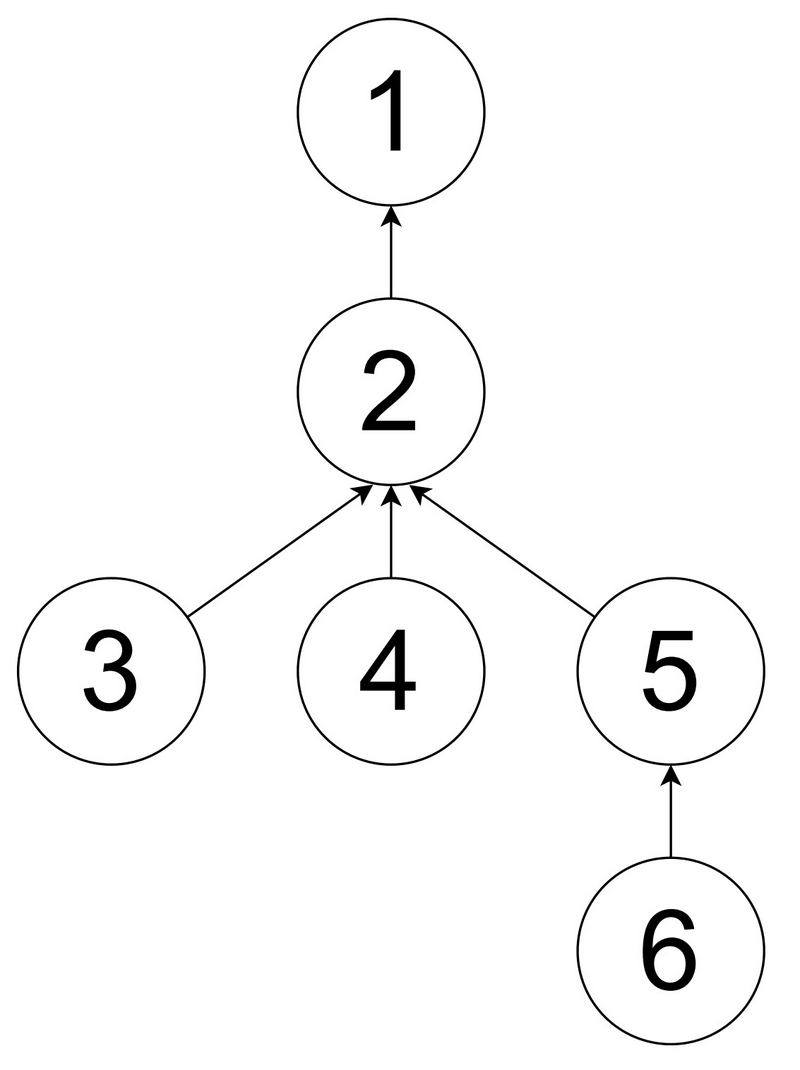
### Sample Explanation 1 $ 1 $ 番目のテストケースについて考えます。  以下のように $ 2 $ 回操作を行うことができます。 - $ (u,v)=(3,5) $ を選ぶ。頂点 $ 3 $ と頂点 $ 5 $ を黒で塗る。 - $ (u,v)=(4,6) $ を選ぶ。頂点 $ 4 $ と頂点 $ 6 $ を黒で塗る。 操作を $ 2 $ 回より多く行うことはできないので、 $ 1 $ 行目には $ 2 $ を出力してください。 ### Constraints - $ 1\le T\le 5\times 10^4 $ - $ 2\le N\le 5\times 10^5 $ - $ 1\le p_i < i $ - 全てのテストケースにおける $ N $ の総和は $ 5\times 10^5 $ 以下 - 入力される値は全て整数